题目内容
若b2=ac，求| a2b2c2 |
| a3+b3+c3 |
| 1 |
| a3 |
| 1 |
| b3 |
| 1 |
| c3 |
分析：先将
(
+
+
)通过对(
+
+
)通分转化为
×
，再将b2=ac（即ac=b2）代入约分化简，约去公因式．最终的值为1
| a2b2c2 |
| a3+b3+c3 |
| 1 |
| a3 |
| 1 |
| b3 |
| 1 |
| c3 |
| 1 |
| a3 |
| 1 |
| b3 |
| 1 |
| c3 |
| a2b2c2 |
| a3+b3+c3 |
| b3c3+a3c3+a3b3 |
| a3b3c3 |
解答：解：
(
+
+
)，
=
×
，
=
×
，
=
×
，
=
，
=
，
=1．
故答案为1．
| a2b2c2 |
| a3+b3+c3 |
| 1 |
| a3 |
| 1 |
| b3 |
| 1 |
| c3 |
=
| a2b2c2 |
| a3+b3+c3 |
| b3c3+a3c3+a3b3 |
| a3b3c3 |
=
| a2b2c2 |
| a3+b3+c3 |
| b3c3+b6+a3b3 |
| a3b3c3 |
=
| 1 |
| a3+b3+c3 |
| b3(c3+b3+a3) |
| abc |
=
| b3 |
| abc |
=
| abc |
| abc |
=1．
故答案为1．
点评：同学们要注意，化简分式方程的过程中一定要有效利用通分、约分．本题再加上b2=ac这个已知条件，可以说是对通分、约分运用的典型．
练习册系列答案
相关题目
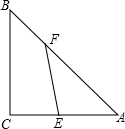已知：如图，在△ABC中，∠A、∠B、∠C所对的边分别为a、b、c．点E是AC边上的一个动点（点E与点A、C不重合），点F是AB边上的一个动点（点F与点A、B不重合），连接EF．
