题目内容
(2012•衢州二模)已知:抛物线y1=x2以点C为顶点且过点B,抛物线y2=a2x2+b2x+c2以点B为顶点且过点C,分别过点B、C作x轴的平行线,交抛物线y1=x2、y2=a2x2+b2x+c2于点A、D,且AB=AC.
(1)如图1,①求证:△ABC为正三角形;②求点A的坐标;
(2)①如图2,若将抛物线“y1=x2”改为“y1=x2+1”,其他条件不变,求CD的长;
②如图3,若将抛物线“y1=x2”改为“y1=3x2+b1x+c1”,其他条件不变,求a2的值;
(3)若将抛物线“y1=x2”改为抛物线“y1=a1x2+b1x+c1”,其他条件不变,直接写出b1关于b2的关系式.
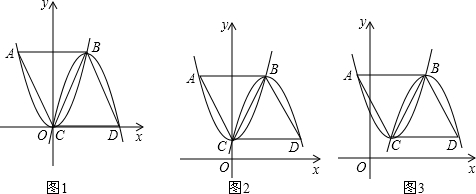
(1)如图1,①求证:△ABC为正三角形;②求点A的坐标;
(2)①如图2,若将抛物线“y1=x2”改为“y1=x2+1”,其他条件不变,求CD的长;
②如图3,若将抛物线“y1=x2”改为“y1=3x2+b1x+c1”,其他条件不变,求a2的值;
(3)若将抛物线“y1=x2”改为抛物线“y1=a1x2+b1x+c1”,其他条件不变,直接写出b1关于b2的关系式.

分析:(1)①由于AB∥x轴,显然点A、B关于抛物线y1=x2的对称轴对称,可得AC=BC,已知AB=AC,那么△ABC必为等边三角形;
②由抛物线y1的解析式设出点A的坐标,再根据△ABC是等边三角形列出点A横、纵坐标的关系式,以此确定点A的坐标.
(2)①若称AB与抛物线y1对称轴的交点为E,可设AE=BE=m(m>0),在等边△ABC中,CE=
m,可用m表示出点B的坐标,代入抛物线解析式中即可求出m的值,则AB的长可求;在(1)的解答过程中,不难看出△ABC、△BCD都是等边三角形,因此由CD=BC=AB即可得解;
②将y1的解析式写成顶点式,即:y1=3(x-h)2+k,首先根据等边△ABC的特点表达出点B的坐标,将点B的坐标代入抛物线y1的解析式中,由此求得m的值;抛物线y2以点B为顶点,可先写成顶点式,再将点A的坐标代入其中来确定a2的值.
(3)由于这个小题并没有说明按给出的三个图求解,所以还需考虑抛物线y2在y1左侧的情况,但解法是相同的,仍以y2在y1右侧为例进行说明:
在(2)①的解答过程中,我们不难看出
CD=
AB=m=
,而
AB的长度正好是两个抛物线对称轴的差的绝对值,那么可以拿
CD的长来作为等量关系列出关系式,据此求得b1、b2的关系式.
②由抛物线y1的解析式设出点A的坐标,再根据△ABC是等边三角形列出点A横、纵坐标的关系式,以此确定点A的坐标.
(2)①若称AB与抛物线y1对称轴的交点为E,可设AE=BE=m(m>0),在等边△ABC中,CE=
| 3 |
②将y1的解析式写成顶点式,即:y1=3(x-h)2+k,首先根据等边△ABC的特点表达出点B的坐标,将点B的坐标代入抛物线y1的解析式中,由此求得m的值;抛物线y2以点B为顶点,可先写成顶点式,再将点A的坐标代入其中来确定a2的值.
(3)由于这个小题并没有说明按给出的三个图求解,所以还需考虑抛物线y2在y1左侧的情况,但解法是相同的,仍以y2在y1右侧为例进行说明:
在(2)①的解答过程中,我们不难看出
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| a1 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)
①证明:∵AB∥x轴,∴A、B关于y轴对称,即AC=BC;
又∵AB=AC,∴AB=AC=BC;
即:△ABC是等边三角形.
②设点A的坐标为(x,x2)(x<0);
在等边△ABC中,x2=tan60°•(-x),解得:x1=0、x2=-
∴A(-
,3).
 (2)设线段AB交抛物线y1的对称轴于点E,AE=BE=m(m>0);
(2)设线段AB交抛物线y1的对称轴于点E,AE=BE=m(m>0);
①如图(2)-①,在Rt△BCE中,BE=m,EC=
m,则B(m,
m+1);
由于点B在y1=x2+1的函数图象上,所以有:
m+1=m2+1,解得:m=
∴AB=2BE=2m=2
;
同(1)①可知,△BCD、△ABC都是等边三角形,则CD=AB=2
.
②设抛物线y1=3x2+b1x+c1=3(x-h)2+k,则C(h,k)、B(h+m,k+
m);
由于点B在y1=3(x-h)2+k上,有:
k+
m=3m2+k,解得:m=
∴B(h+
,k+1);
则抛物线y2=a2(x-h-
)2+k+1,代入C(h,k),得:
a2×
+k+1=k,解得:a2=-3.

(3)由(2)②知,a2=-a1;
由(2)①知,
CD=
AB=m=|-
-(-
)|=|
|,
而m=|
|(由(2)的解答过程可知),则:
|
|=|
|,解得:b1+b2=±2
;
即:b1=2
-b2或 b1=-2
-b2.
①证明:∵AB∥x轴,∴A、B关于y轴对称,即AC=BC;
又∵AB=AC,∴AB=AC=BC;
即:△ABC是等边三角形.
②设点A的坐标为(x,x2)(x<0);
在等边△ABC中,x2=tan60°•(-x),解得:x1=0、x2=-
| 3 |
∴A(-
| 3 |
 (2)设线段AB交抛物线y1的对称轴于点E,AE=BE=m(m>0);
(2)设线段AB交抛物线y1的对称轴于点E,AE=BE=m(m>0);①如图(2)-①,在Rt△BCE中,BE=m,EC=
| 3 |
| 3 |
由于点B在y1=x2+1的函数图象上,所以有:
| 3 |
| 3 |
∴AB=2BE=2m=2
| 3 |
同(1)①可知,△BCD、△ABC都是等边三角形,则CD=AB=2
| 3 |
②设抛物线y1=3x2+b1x+c1=3(x-h)2+k,则C(h,k)、B(h+m,k+
| 3 |
由于点B在y1=3(x-h)2+k上,有:
k+
| 3 |
| ||
| 3 |
∴B(h+
| ||
| 3 |
则抛物线y2=a2(x-h-
| ||
| 3 |
a2×
| 1 |
| 3 |

(3)由(2)②知,a2=-a1;
由(2)①知,
| 1 |
| 2 |
| 1 |
| 2 |
| b1 |
| 2a1 |
| b2 |
| 2a2 |
| b1+b2 |
| 2a1 |
而m=|
| ||
| a1 |
|
| b1+b2 |
| 2a1 |
| ||
| a1 |
| 3 |
即:b1=2
| 3 |
| 3 |
点评:该题是二次函数与等边三角形的综合题;随着题目的深入,y1解析式逐渐变的复杂,这也是题目的难点所在,只要抓住题目难度的递进性,能够把(2)的解答过程理解透彻,也就能掌握这道题的解题思路和方法;在解题过程中,要抓住等边三角形和两个抛物线顶点这三个关键条件,而最后一题中,没有明示按给出的三个图来解是容易丢解的地方.

练习册系列答案
相关题目
 (2012•衢州二模)如图是某区“平改坡”工程中一种坡屋顶的设计图.已知原平屋顶的宽度AB为8米,两条相等的斜面钢条AC、BC夹角为110°,过点C作CD⊥AB于D.
(2012•衢州二模)如图是某区“平改坡”工程中一种坡屋顶的设计图.已知原平屋顶的宽度AB为8米,两条相等的斜面钢条AC、BC夹角为110°,过点C作CD⊥AB于D. 、乙两班离A地的距离分别为y1千米、y2千米,y1、y2与x的函数关系图象如图所示,根据图象解答下列问题:
、乙两班离A地的距离分别为y1千米、y2千米,y1、y2与x的函数关系图象如图所示,根据图象解答下列问题: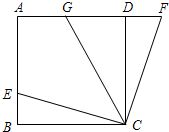 (2012•衢州二模)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE=
(2012•衢州二模)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE=