题目内容
17.直角坐标系中,四边形ABCD的顶点坐标依次为A(-1,0),B(a,b),C(-1,5),D(c,d)(1)当四边形ABCD是菱形时,求a,b,c,d应满足的条件;
(2)四边形ABCD是正方形时,求a,c的值;
(3)当点D在y轴上,且四边形ABCD是矩形时,求点D的坐标.
分析 (1)由菱形的对角线互相垂直平分,容易得出结果;
(2)根据正方形的性质得出a、c的关系式,再由(1)的结果即可得出a、c的值;
(3)证明三角形相似得出比例式即可得出结果.
解答 解:(1)∵A(-1,0),C(-1,5),
∴AC=5,OA=1,
∵四边形ABCD是菱形
∴对角线AC、BD互相垂直平分,
∴b=d=$\frac{5}{2}$,a+c=-2;
(2)∵四边形ABCD是正方形,
∴AC=BD,
∴c-a=5,
又∵a+c=-2,
∴c=$\frac{3}{2}$,a=-$\frac{7}{2}$;
(3)如图所示:
∵四边形ABCD是矩形,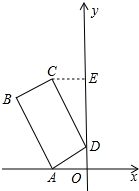 ∴∠ADC=90°
∴∠ADC=90°
∵∠ECD+∠EDC=∠ADO+∠EDC=90°,
∴∠ECD=∠ADO,又∵∠CED=∠DOA
∴△CED∽△DOA,
∴$\frac{CE}{OD}$=$\frac{DE}{AO}$,即$\frac{1}{OD}$=$\frac{5-OD}{1}$,
解得:OD=$\frac{{5±\sqrt{21}}}{2}$
即点D的坐标为(0,$\frac{{5+\sqrt{21}}}{2}$)或(0,$\frac{{5-\sqrt{21}}}{2}$).
点评 本题考查了正方形的性质、菱形的性质、坐标与图形性质、矩形的性质;熟练掌握特殊平行四边形的性质是解题的关键;特别是(3)中,通过证明三角形相似得出比例式得出结果.

练习册系列答案
相关题目
5.已知y1=x2-3x+2,y2=2x+8,设函数H=max{y1,y2},G=min{y1,y2}.( max{a,b}表示a,b中较大的数,min{a,b}表示a,b中较小的数.比如max{-1,3}=3,min{-1,3}=-1).则下列结论中正确的是( )
| A. | H有最大值20 | B. | H有最小值6 | C. | G有最小值6 | D. | G有最大值20 |
6.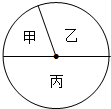 学校“沥园文学”社成员来自初一、初二、初三三个年级的学生,其人数比为2:3:5,如图所示的扇形图表示上述分布情况.已知来自初一的学生为10人,则下列说法不正确的是( )
学校“沥园文学”社成员来自初一、初二、初三三个年级的学生,其人数比为2:3:5,如图所示的扇形图表示上述分布情况.已知来自初一的学生为10人,则下列说法不正确的是( )
 学校“沥园文学”社成员来自初一、初二、初三三个年级的学生,其人数比为2:3:5,如图所示的扇形图表示上述分布情况.已知来自初一的学生为10人,则下列说法不正确的是( )
学校“沥园文学”社成员来自初一、初二、初三三个年级的学生,其人数比为2:3:5,如图所示的扇形图表示上述分布情况.已知来自初一的学生为10人,则下列说法不正确的是( )| A. | 扇形甲的圆心角是72° | B. | 学生的总人数是90人 | ||
| C. | 初三的人数比初二的人数多10人 | D. | 初一的人数比初三的人数少15人 |
7.下列运算中正确的是( )
| A. | a2+a3=a5 | B. | a2•a4=a8 | C. | (a2)3=a5 | D. | a6÷a2=a4 |
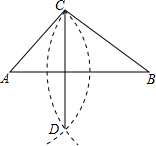 已知,△ABC,按如下步骤作图:
已知,△ABC,按如下步骤作图: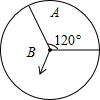 如图,有一转盘中有A、B两个区域,A区域所对的圆心角为120°,让转盘自由转动两次.则两次指针都落在A区域的概率为$\frac{1}{9}$.
如图,有一转盘中有A、B两个区域,A区域所对的圆心角为120°,让转盘自由转动两次.则两次指针都落在A区域的概率为$\frac{1}{9}$.