题目内容
9．
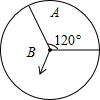如图，有一转盘中有A、B两个区域，A区域所对的圆心角为120°，让转盘自由转动两次．则两次指针都落在A区域的概率为$\frac{1}{9}$．
分析 首先将B区域平分成两部分，然后根据题意画树状图，由树状图求得所有等可能的结果与两次指针都落在A区域的情况，再利用概率公式即可求得答案．
解答 解：将B区域平分成两部分，
画树状图得：
∵共有9种等可能的结果，两次指针都落在A区域的只有1种情况，
∴两次指针都落在A区域的概率为：$\frac{1}{9}$．
故答案为：$\frac{1}{9}$．
点评 此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
19．
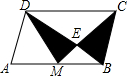如图，已知M为平行四边形ABCD的边AB的中点，CM交BD于点E，BD=3BE，则图中阴影部分的面积与平行四边形ABCD面积的比是（ ）
如图，已知M为平行四边形ABCD的边AB的中点，CM交BD于点E，BD=3BE，则图中阴影部分的面积与平行四边形ABCD面积的比是（ ）| A． | 1：2 | B． | 2：5 | C． | 3：5 | D． | 1：3 |
14．
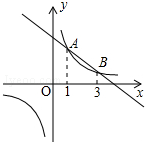如图，在平面直角坐标系中，反比例函数y1=$\frac{3}{x}$的图象与一次函数y2=kx+b的图象交于A、B两点．若y1＜y2，则x的取值范围是（ ）
如图，在平面直角坐标系中，反比例函数y1=$\frac{3}{x}$的图象与一次函数y2=kx+b的图象交于A、B两点．若y1＜y2，则x的取值范围是（ ）| A． | 1＜x＜3 | B． | x＜0或1＜x＜3 | C． | 0＜x＜1 | D． | x＞3或0＜x＜1 |
1．
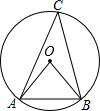如图，圆O中，AO=5，弦AB长为8．C为弦AB所对优弧上的一点，求∠C的正切值（ ）
如图，圆O中，AO=5，弦AB长为8．C为弦AB所对优弧上的一点，求∠C的正切值（ ）| A． | $\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
19．
如图所示，∠β＞∠α，且∠α与$\frac{1}{2}$（∠β-∠α）关系为（ ）
如图所示，∠β＞∠α，且∠α与$\frac{1}{2}$（∠β-∠α）关系为（ ）| A． | 互补 | B． | 互余 | C． | 和为45° | D． | 和为22.5° |