题目内容
2.当x满足$\left\{\begin{array}{l}x+1>3x-3\\ \frac{1}{2}(x-\frac{1}{2})>\frac{1}{3}(x-\frac{1}{2})\end{array}\right.$,求出分式方程$\frac{x}{x-1}$-1=$\frac{3}{(x-1)(x+2)}$的解.分析 求出不等式组的解集确定出x的范围,分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:不等式组$\left\{\begin{array}{l}{x+1>3x-3①}\\{\frac{1}{2}(x-\frac{1}{2})>\frac{1}{3}(x-\frac{1}{2})②}\end{array}\right.$,
由①得:x<2;
由②得:x>$\frac{1}{2}$,
不等式组的解集为:$\frac{1}{2}$<x<2,
分式方程去分母得:x2+2x-x2-2x+x+2=3,
解得:x=1,
经检验:x=1是增根,原方程无解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
12.某公司欲招聘一名公关人员,对甲、乙两位候选人进行了面试和笔试,他们的成绩如表所示:
根据需要,面试的成绩与笔试按6:4的比例确定个人成绩(成绩高者被录用),那么谁将被录用?
| 候选人 | 测试成绩(百分制) | |
| 面试 | 笔试 | |
| 甲 | 85 | 95 |
| 乙 | 95 | 83 |
13.我们知道$\sqrt{19}$是个无理数,$\sqrt{19}$-1在哪两个整数之间( )
| A. | 1与2 | B. | 2与3 | C. | 3与4 | D. | 4与5 |
7.在算式$\sqrt{2011}$×$\sqrt{2012}$×$\sqrt{2013}$×$\sqrt{2014}$中,你估计哪一个因数值减小1导致乘积减小最大( )
| A. | $\sqrt{2011}$ | B. | $\sqrt{2012}$ | C. | $\sqrt{2013}$ | D. | $\sqrt{2014}$ |
14.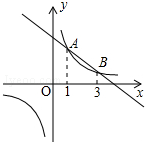 如图,在平面直角坐标系中,反比例函数y1=$\frac{3}{x}$的图象与一次函数y2=kx+b的图象交于A、B两点.若y1<y2,则x的取值范围是( )
如图,在平面直角坐标系中,反比例函数y1=$\frac{3}{x}$的图象与一次函数y2=kx+b的图象交于A、B两点.若y1<y2,则x的取值范围是( )
 如图,在平面直角坐标系中,反比例函数y1=$\frac{3}{x}$的图象与一次函数y2=kx+b的图象交于A、B两点.若y1<y2,则x的取值范围是( )
如图,在平面直角坐标系中,反比例函数y1=$\frac{3}{x}$的图象与一次函数y2=kx+b的图象交于A、B两点.若y1<y2,则x的取值范围是( )| A. | 1<x<3 | B. | x<0或1<x<3 | C. | 0<x<1 | D. | x>3或0<x<1 |
11.为奖励大学生创业,我市为在开发区创业的每位大学生提供无息贷款145000元,这个数据用科学记数法表示为(精确到万元)( )
| A. | 1.45×105 | B. | 1.5×105 | C. | 1.4×105 | D. | 1.5×106 |