题目内容
13．已知：∠A是锐角且满足sinA=$\frac{5}{13}$，则sin（90°-A）=$\frac{12}{13}$．分析 根据题意画出图形，利用勾股定理求出AB的长，进而可得出结论．
解答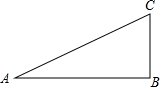 
解：如图，∵∠A是锐角且满足sinA=$\frac{5}{13}$，
∴设BC=5x，则AC=13x，
∵AC2=BC2+AB2，
∴AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{（13x）^{2}-（5x）^{2}}$=12x，
∴sin（90°-A）=cosA=$\frac{AB}{AC}$=$\frac{12x}{13x}$=$\frac{12}{13}$．
故答案为：$\frac{12}{13}$．
点评 本题考查的是互余两角三角函数关系，熟知一个角的正弦值等于这个角的余角的余弦值是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，从公园甲到公园乙的三条路线中，最短的是（3），这是因为两点之间线段最短．
反比例函数的图象如图所示，则k的值可能0.5．（写出一个即可）
5．为了比较两箱樱桃的个头大小，分别在两箱樱桃中随机抽出若干颗樱桃，统计其质量（单位：g）如下表：
从樱桃的大小及匀称角度看，更好的一箱是甲箱．
表1：甲箱樱桃抽检结果
表2：乙箱樱桃的抽检结果
从樱桃的大小及匀称角度看，更好的一箱是甲箱．
表1：甲箱樱桃抽检结果
| 质量 | 8 | 9 | 10 | 11 | 12 |
| 颗数 | 0 | 3 | 5 | 3 | 1 |
| 质量 | 7 | 9 | 10 | 11 | 12 |
| 颗数 | 1 | 1 | 5 | 4 | 1 |