题目内容
 如图,在⊙O中,AD、BC相交于点E,OE平分∠AEC.
如图,在⊙O中,AD、BC相交于点E,OE平分∠AEC.
(1)求证:AB=CD;
(2)如果⊙O的半径为5,AD⊥CB,DE=1,求AD的长.
证明:(1)过点O作OM⊥AD,ON⊥BC,

∵OE平分∠AEC,
∴OM=ON,
∴ =
= ,
, -
- =
= -
- ,即
,即 ,
,
∴AB=CD.
(2)∵OM⊥AD,
∴AM=DM,
∵AD⊥CB,OE平分∠AEC,
∴∠OEM=45°,
∴∠OME=45°,
∴∠OEM=∠EOM,
∴OM=ME,
在Rt△AOM中,OA2=OM2+AM2,即25=(AM-1)2+AM2,
解得:AM=4或AM=-3(舍去)
故AD的长为8.
分析:(1)过点O作OM⊥AD,ON⊥BC,从而得出OM=ON,根据垂径定理可得出 =
= ,然后可得
,然后可得 =
= ,继而得出结论.
,继而得出结论.
(2)先判断OM=ME,然后利用勾股定理得出AM的方程,解出后,根据AD=2AM,即可得出答案.
点评:本题考查了勾股定理、垂径定理及圆心角、弧、弦之间的关系,属于基础题,注意一些基本定理及性质的掌握.

∵OE平分∠AEC,
∴OM=ON,
∴
 =
= ,
, -
- =
= -
- ,即
,即 ,
,∴AB=CD.
(2)∵OM⊥AD,
∴AM=DM,
∵AD⊥CB,OE平分∠AEC,
∴∠OEM=45°,
∴∠OME=45°,
∴∠OEM=∠EOM,
∴OM=ME,
在Rt△AOM中,OA2=OM2+AM2,即25=(AM-1)2+AM2,
解得:AM=4或AM=-3(舍去)
故AD的长为8.
分析:(1)过点O作OM⊥AD,ON⊥BC,从而得出OM=ON,根据垂径定理可得出
 =
= ,然后可得
,然后可得 =
= ,继而得出结论.
,继而得出结论.(2)先判断OM=ME,然后利用勾股定理得出AM的方程,解出后,根据AD=2AM,即可得出答案.
点评:本题考查了勾股定理、垂径定理及圆心角、弧、弦之间的关系,属于基础题,注意一些基本定理及性质的掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
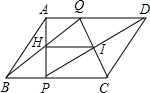 如图,在?ABCD中,AD=6cm,点P、Q分别是边BC、AD上的动点,点P以一定的速度沿BC从B向C匀速运动,与此同时点Q以相同的速度沿AD从A向D运动,连接AP、PD、BQ、CQ、AP、BQ交于点H,PD、CQ交于点I,连接HI.试猜想:在运动的过程中,HI的长度是否变化?若变化,请说明理由;若不变,请求出HI的长度?
如图,在?ABCD中,AD=6cm,点P、Q分别是边BC、AD上的动点,点P以一定的速度沿BC从B向C匀速运动,与此同时点Q以相同的速度沿AD从A向D运动,连接AP、PD、BQ、CQ、AP、BQ交于点H,PD、CQ交于点I,连接HI.试猜想:在运动的过程中,HI的长度是否变化?若变化,请说明理由;若不变,请求出HI的长度? (2013•哈尔滨)如图,在?ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为( )
(2013•哈尔滨)如图,在?ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为( ) 如图,在△ABC中,AD=3,AB=4
如图,在△ABC中,AD=3,AB=4 如图,在△ABC中,AD=DE,AB=BE,∠CED=70°,则∠A=
如图,在△ABC中,AD=DE,AB=BE,∠CED=70°,则∠A= 如图,在ABC中,AD平分∠BAC,AE:AC=AF:AB=1:3,那么AG:GD的值为( )
如图,在ABC中,AD平分∠BAC,AE:AC=AF:AB=1:3,那么AG:GD的值为( )