题目内容
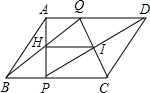 如图,在?ABCD中,AD=6cm,点P、Q分别是边BC、AD上的动点,点P以一定的速度沿BC从B向C匀速运动,与此同时点Q以相同的速度沿AD从A向D运动,连接AP、PD、BQ、CQ、AP、BQ交于点H,PD、CQ交于点I,连接HI.试猜想:在运动的过程中,HI的长度是否变化?若变化,请说明理由;若不变,请求出HI的长度?
如图,在?ABCD中,AD=6cm,点P、Q分别是边BC、AD上的动点,点P以一定的速度沿BC从B向C匀速运动,与此同时点Q以相同的速度沿AD从A向D运动,连接AP、PD、BQ、CQ、AP、BQ交于点H,PD、CQ交于点I,连接HI.试猜想:在运动的过程中,HI的长度是否变化?若变化,请说明理由;若不变,请求出HI的长度?
分析:因为P、Q同时以相同的速度运动,所以连接PQ,四边形ABPQ和四边形PQDC均为平行四边形,根据平行四边形对角线互相平分,H、I分别是AP、PQ的中点,再根据三角形的中位线平行于第三边并且等于第三边的一半可得HI=
AD,所以运动过程中长度不变.
| 1 |
| 2 |
解答: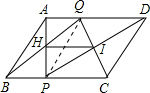 解:HI的长度不变,为3cm.
解:HI的长度不变,为3cm.
由题意得AQ=BP,DQ=PC,连接PQ,
又∵AQ∥BP,QD∥PC,
∴四边形ABPQ、四边形PQDC均为平行四边形,
∴AH=HP,DI=PI,
∴在△APD中,HI=
AD=
×6=3cm.
 解:HI的长度不变,为3cm.
解:HI的长度不变,为3cm.由题意得AQ=BP,DQ=PC,连接PQ,
又∵AQ∥BP,QD∥PC,
∴四边形ABPQ、四边形PQDC均为平行四边形,
∴AH=HP,DI=PI,
∴在△APD中,HI=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要利用平行四边形的判定和三角形的中位线定理求解,把运动中的量转化为不变的量的一部分是解此类题目常用的方法.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB=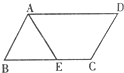 18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.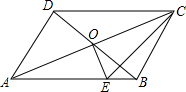 如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是
如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是