题目内容
已知,平面直角坐标系中,A在x轴正半轴,B(0,1),AB=2.
(1)如图1,求∠OAB的度数;
(2)如图2,以AB为边作等边△ABE,AD⊥AB交OA的垂直平分线于D,求证:BD=OE;
(3)如图3,在(2)的条件下,DE交AB于F,求
的值.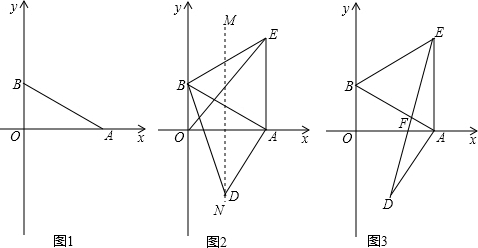
(1)如图1,求∠OAB的度数;
(2)如图2,以AB为边作等边△ABE,AD⊥AB交OA的垂直平分线于D,求证:BD=OE;
(3)如图3,在(2)的条件下,DE交AB于F,求
| DF |
| EF |

考点:全等三角形的判定与性质,坐标与图形性质,等边三角形的判定与性质
专题:
分析:(1)由条件可知AB=2OB,可知∠OAB=30°;
(2)连接OD,易证△ADO为等边三角形,再证△ABD≌△AEO即可;
(3)作EH⊥AB于H,先证△ABO≌△AEH,得AO=EH,再证△AFD≌△EFH,可得DF=EF,可求得比值.
(2)连接OD,易证△ADO为等边三角形,再证△ABD≌△AEO即可;
(3)作EH⊥AB于H,先证△ABO≌△AEH,得AO=EH,再证△AFD≌△EFH,可得DF=EF,可求得比值.
解答:(1)解:
在Rt△ABO中,AB=2,OB=1,
∴sin∠OAB=
=
,
∴∠OAB=30°;
(2)证明:连接OD,如图1,
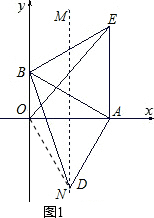
∵∠BAO=30°,作OA的垂直平分线MN交AB的垂线AD于点D,
∴∠DAO=60°,
又DO=DA,
∴△ADO为等边三角形.
∴DA=AO,
在△ABD和△AEO中
∴△ABD≌△AEO(SAS),
∴BD=OE.
(3)证明:如图2,作EH⊥AB于H.
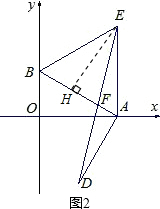
∵AE=AB,BO=
AB,
∴AH=BO,
在Rt△ABO和Rt△AEH中,
,
∴Rt△ABO≌Rt△AEH(HL),
∴AO=EH=AD.
又∠EHF=∠DAF=90°,
在△AFD和△EFH中,
∴△AFD≌△EFH(AAS),
∴EF=DF,
∴
=1.
在Rt△ABO中,AB=2,OB=1,
∴sin∠OAB=
| OB |
| AB |
| 1 |
| 2 |
∴∠OAB=30°;
(2)证明:连接OD,如图1,

∵∠BAO=30°,作OA的垂直平分线MN交AB的垂线AD于点D,
∴∠DAO=60°,
又DO=DA,
∴△ADO为等边三角形.
∴DA=AO,
在△ABD和△AEO中
|
∴△ABD≌△AEO(SAS),
∴BD=OE.
(3)证明:如图2,作EH⊥AB于H.

∵AE=AB,BO=
| 1 |
| 2 |
∴AH=BO,
在Rt△ABO和Rt△AEH中,
|
∴Rt△ABO≌Rt△AEH(HL),
∴AO=EH=AD.
又∠EHF=∠DAF=90°,
在△AFD和△EFH中,
|
∴△AFD≌△EFH(AAS),
∴EF=DF,
∴
| DF |
| EF |
点评:本题主要考查全等三角形的判定和性质及等边三角形的判定和性质,解题时注意构造三角形全等从而找到线段相等是解题的关键,知识点较多,难度较大.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
甲,乙,丙三辆卡车所运货物的质量之比为6:7:4.5,已知甲车比乙车少运货物12吨,则三辆卡车公运货物( )
| A、120吨 | B、130吨 |
| C、210吨 | D、150吨 |

 在如图两个等圆的转盘上设计一个配紫色游戏,使配紫色的概率为
在如图两个等圆的转盘上设计一个配紫色游戏,使配紫色的概率为 在△ABC中,∠ABC、∠ACB的外角平分线BP、CP交于点P.
在△ABC中,∠ABC、∠ACB的外角平分线BP、CP交于点P.