题目内容
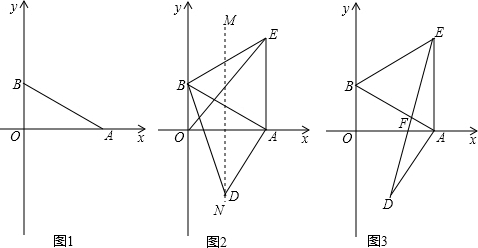
如图,已知△CDE中,∠CED=120°,直线l经过点E,点B是直线l上任意一点,连接BD,过点C作CA∥BD交于点A.

(1)如图①,当点B在E点左侧时,求证:∠BDE+∠ACE=120°;
(2)如图②,当点B在E点右侧时,画出图形,并直接写出∠BDE,∠ACE的数量关系;
(3)在(2)的条件下,作∠ACE的角平分线交直线DE于点F,∠EDB=20°,求∠CFD的大小.

(1)如图①,当点B在E点左侧时,求证:∠BDE+∠ACE=120°;
(2)如图②,当点B在E点右侧时,画出图形,并直接写出∠BDE,∠ACE的数量关系;
(3)在(2)的条件下,作∠ACE的角平分线交直线DE于点F,∠EDB=20°,求∠CFD的大小.
考点:平行线的性质
专题:
分析:(1)过E作EF∥DB,根据平行线的性质可得∠ACE=∠FEC,∠DBE=∠DEF,进而可得答案;
(2)根据平行线的性质可得∠1=∠ACE,根据三角形内角与外角的性质可得∠BDE+∠DEC=∠1,再利用等量代换可得∠BDE+120°=∠ACE,进而可得答案;
(3)根据题意画出图形,可求出∠ECA的度数,再根据角平分线的性质可得∠ECF,再利用三角形内角和定理可算出∠CFD.
(2)根据平行线的性质可得∠1=∠ACE,根据三角形内角与外角的性质可得∠BDE+∠DEC=∠1,再利用等量代换可得∠BDE+120°=∠ACE,进而可得答案;
(3)根据题意画出图形,可求出∠ECA的度数,再根据角平分线的性质可得∠ECF,再利用三角形内角和定理可算出∠CFD.
解答:(1)证明:过E作EF∥DB,
∵CA∥BD,
∴∠ACE=∠FEC,
∵DB∥EF,
∴∠DBE=∠DEF,
∴∠BDE+∠ACE=∠DEF+∠FEC=120°;
(2)∵CA∥BD,
∴∠1=∠ACE,
∵∠BDE+∠DEC=∠1,
∵∠CED=120°,
∴∠BDE+120°=∠ACE,
∴∠ACE-∠BDE=120°;
(3)∵∠EDB=20°,
∴∠ACE=140°,
∵CF平分∠ACE,
∴∠ECF=70°,
∵∠DEC=120°,
∴∠CEF=60°,
∴∠CFD=180°-60°-70°=50°.
∵CA∥BD,
∴∠ACE=∠FEC,

∵DB∥EF,
∴∠DBE=∠DEF,
∴∠BDE+∠ACE=∠DEF+∠FEC=120°;
(2)∵CA∥BD,
∴∠1=∠ACE,
∵∠BDE+∠DEC=∠1,
∵∠CED=120°,
∴∠BDE+120°=∠ACE,
∴∠ACE-∠BDE=120°;
(3)∵∠EDB=20°,
∴∠ACE=140°,
∵CF平分∠ACE,
∴∠ECF=70°,
∵∠DEC=120°,
∴∠CEF=60°,
∴∠CFD=180°-60°-70°=50°.
点评:此题主要考查了平行线的性质,以及三角形内角和定理与外角的关系,关键是掌握两直线平行,内错角相等.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
已知OA是⊙O的半径,若CD⊥OA,则以下说法正确的是( )
| A、CD⊙O的切线 |
| B、CD与⊙O相离 |
| C、CD与⊙O相切 |
| D、不能确定 |
∠A与∠B互为补角,且∠A>∠B,那么∠B的余角等于( )
A、
| ||
| B、∠A+∠B | ||
C、
| ||
D、
|
 如图所示的几何体,从左向右看到的平面图形是( )
如图所示的几何体,从左向右看到的平面图形是( )A、 |
B、 |
C、 |
D、 |