题目内容
(2009•宝安区二模)如图,以锐角△CDE的边CD、DE为边长向外分别作正方形ABCD和DEFG,连接AE和CG,交于点H,CG与DE交于点K.(1)求证:AE=CG;
(2)求证:DG•EK=GK•HE.
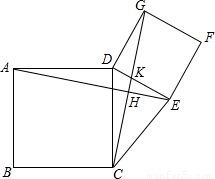
【答案】分析:(1)要证明AE=CG可以通过证明△ADE≌△CDG得到,而△ADE≌△CDG容易根据正方形的性质得到全等条件,所以这样可以解决问题;
(2)根据(1)可以得到∠AED=∠CGD,再根据已知条件容易证明△HKE∽△DKG,再利用相似三角形的性质可以得到结论;
解答:证明:(1)∵四边形ABCD与DEFG是正方形,
∴AD=CD,DE=DG,∠ADC=∠EDG.(1分)
∴∠ADC+∠CDE=∠EDG+∠CDE.
即:∠ADE=∠CDG.(2分)
∴△ADE≌△CDG.(3分)
∴AE=CG.(4分)
(2)∵△ADE≌△CDG,
∴∠AED=∠CGD.
∵∠EKH=∠DKG,
∴△HKE∽△DKG.(6分)
∴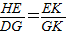 .(7分)
.(7分)
∴DG•EK=GK•HE.(8分)
点评:此题分别考查了全等三角形的性质与判定,相似三角形的判定与性质,综合利用它们解决问题.
(2)根据(1)可以得到∠AED=∠CGD,再根据已知条件容易证明△HKE∽△DKG,再利用相似三角形的性质可以得到结论;
解答:证明:(1)∵四边形ABCD与DEFG是正方形,
∴AD=CD,DE=DG,∠ADC=∠EDG.(1分)
∴∠ADC+∠CDE=∠EDG+∠CDE.
即:∠ADE=∠CDG.(2分)
∴△ADE≌△CDG.(3分)
∴AE=CG.(4分)
(2)∵△ADE≌△CDG,
∴∠AED=∠CGD.
∵∠EKH=∠DKG,
∴△HKE∽△DKG.(6分)
∴
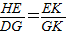 .(7分)
.(7分)∴DG•EK=GK•HE.(8分)
点评:此题分别考查了全等三角形的性质与判定,相似三角形的判定与性质,综合利用它们解决问题.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
(2009•宝安区二模)在2008年深圳读书节活动期间,为了了解学校初三年级学生的课外阅读情况,小颖随机抽取初三年级部分同学进行调查,把得到的数据处理后制成如下的表格,并绘制成如图所示的统计图,请根据表格和统计图,解答如下问题:
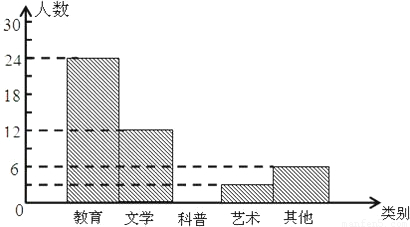
(1)小颖所采用的调查方式是______;
(2)补全图中的频数分布直方图;
(3)从被调查的同学中随机选取一位同学,则选取的恰是在课外阅读教育类书籍的同学的概率是______;
(4)如果该校初三年级共有学生600人,那么课外阅读文学类书籍的学生人数大约是______人.
| 书籍类别 | 教育 | 文学 | 科普 | 艺术 | 其它 |
| 人数 | 24 | 12 | 15 | 3 | 6 |

(1)小颖所采用的调查方式是______;
(2)补全图中的频数分布直方图;
(3)从被调查的同学中随机选取一位同学,则选取的恰是在课外阅读教育类书籍的同学的概率是______;
(4)如果该校初三年级共有学生600人,那么课外阅读文学类书籍的学生人数大约是______人.
 ,0)时,x轴上是否存在两点P、Q(点P在点Q的左边),使得四边形PQDA是菱形?若存在,请求出符合条件的所有点P的坐标;若不存在,请说明理由.
,0)时,x轴上是否存在两点P、Q(点P在点Q的左边),使得四边形PQDA是菱形?若存在,请求出符合条件的所有点P的坐标;若不存在,请说明理由.