题目内容
7.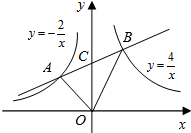 如图,点A是反比例函数y=-$\frac{2}{x}$在第二象限内图象上一点,点B是反比例函数y=$\frac{4}{x}$在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,求△AOB的面积.
如图,点A是反比例函数y=-$\frac{2}{x}$在第二象限内图象上一点,点B是反比例函数y=$\frac{4}{x}$在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,求△AOB的面积.
分析 分别过A、B两点作x轴的垂线,构成直角梯形,根据AC=BC,判断OC为直角梯形的中位线,得出OD=OE=a,根据双曲线解析式确定A、B两点的坐标及AD、BE的长,根据S△AOB=S梯形ADBE-S△AOD-S△BOE求解.
解答 解:分别过A、B两点作AD⊥x轴,BE⊥x轴,垂足为D、E,
∵AC=CB,∴OD=OE,
设A(-a,$\frac{2}{a}$),则B(a,$\frac{4}{a}$),
故S△AOB=S梯形ADBE-S△AOD-S△BOE
=$\frac{1}{2}$($\frac{2}{a}$+$\frac{4}{a}$)×2a-$\frac{1}{2}$a×$\frac{2}{a}$-$\frac{1}{2}$a×$\frac{4}{a}$=3.
点评 本题考查了反比例函数的综合运用.关键是作辅助线构造直角梯形,根据AC=BC,得出OC为直角梯形的中位线,利用面积的和差关系求解.

练习册系列答案
相关题目
18.如果am=3,an=6,则a2m+n等于( )
| A. | 15 | B. | 36 | C. | 12 | D. | 54 |
12. 如图,AB∥CD∥EF,且CG∥AF,则图中与∠CGE相等的角共有( )个.
如图,AB∥CD∥EF,且CG∥AF,则图中与∠CGE相等的角共有( )个.
 如图,AB∥CD∥EF,且CG∥AF,则图中与∠CGE相等的角共有( )个.
如图,AB∥CD∥EF,且CG∥AF,则图中与∠CGE相等的角共有( )个.| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
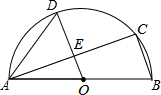 如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.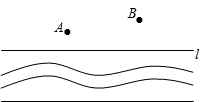 如图,政府决定实施“引河入村”的工程,需将河水经A村引入B村,要使修渠路线最短,水泵站的位置P应建在河边的什么地方,并画出水渠的修建路线.
如图,政府决定实施“引河入村”的工程,需将河水经A村引入B村,要使修渠路线最短,水泵站的位置P应建在河边的什么地方,并画出水渠的修建路线.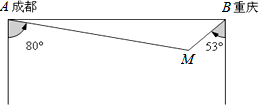
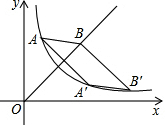 如图所示是反比例函数y=$\frac{k}{x}$(x>0)与正比例函数y=x(x≥0)的图象,点A(1,4)与点B′均在反比例函数的图象上,点B在直线y=x上,点A′是点A关于直线y=x的对称点,四边形AA′B′B是平行四边形.
如图所示是反比例函数y=$\frac{k}{x}$(x>0)与正比例函数y=x(x≥0)的图象,点A(1,4)与点B′均在反比例函数的图象上,点B在直线y=x上,点A′是点A关于直线y=x的对称点,四边形AA′B′B是平行四边形.