题目内容
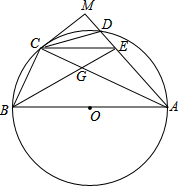 如图:D是以AB为直径的圆O上任意一点,且不与点A、B重合,点C是弧BD的中点,作CE∥AB,交AD或其延长线于E,连接BE交AC与G,AE=CE,过C作CM⊥AD交AD延长线于点M,MC与⊙O相切,CE=7,CD=6,求EG的长.
如图:D是以AB为直径的圆O上任意一点,且不与点A、B重合,点C是弧BD的中点,作CE∥AB,交AD或其延长线于E,连接BE交AC与G,AE=CE,过C作CM⊥AD交AD延长线于点M,MC与⊙O相切,CE=7,CD=6,求EG的长.考点:正弦定理与余弦定理,勾股定理,平行四边形的判定与性质,圆心角、弧、弦的关系,圆周角定理,切线的性质,相似三角形的判定与性质,锐角三角函数的定义
专题:综合题
分析:连接OC,易证四边形AOCE是平行四边形,则有OA=CE=7,由点C是弧BD的中点可得BC=CD=6,运用勾股定理求出AC.由CE∥AB可得△CGE∽△AGB,运用相似三角形的性质可求出AG的长.在Rt△ACB中根据三角函数的定义可求出cos∠BAC,由点C是弧BD的中点可得∠BAC=∠EAG,从而可得到cos∠EAG的值,然后在△EAG中运用余弦定理就可求出EG的长.
解答:解:连接OC,如图.
∵MC与⊙O相切,
∴OC⊥MC.
∵CM⊥AD,
∴OC∥AM.
∵CE∥AB,
∴四边形AOCE是平行四边形,
∴OA=CE=7,
∴AB=14.
∵点C是弧BD的中点,
∴BC=CD=6.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴AC=
=
=4
.
∵CE∥AB,∴△CGE∽△AGB,
∴
=
=
=
,
∴AG=
AC=
.
在Rt△ACB中,
cos∠BAC=
=
=
.
∵点C是弧BD的中点,
∴∠BAC=∠CAD,即∠BAC=∠EAG,
∴cos∠EAG=
.
在△EAG中,
cos∠EAG=
.
∴
=
.
∵AG=
,AE=CE=7,
∴
=
.
整理得:GE2=
.
∵GE>0,∴GE=
.
∴EG的长为
.
∵MC与⊙O相切,
∴OC⊥MC.
∵CM⊥AD,
∴OC∥AM.
∵CE∥AB,
∴四边形AOCE是平行四边形,
∴OA=CE=7,
∴AB=14.
∵点C是弧BD的中点,
∴BC=CD=6.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴AC=
| AB2-BC2 |
| 142-62 |
| 10 |

∵CE∥AB,∴△CGE∽△AGB,
∴
| CG |
| AG |
| CE |
| AB |
| 7 |
| 14 |
| 1 |
| 2 |
∴AG=
| 2 |
| 3 |
8
| ||
| 3 |
在Rt△ACB中,
cos∠BAC=
| AC |
| AB |
4
| ||
| 14 |
2
| ||
| 7 |
∵点C是弧BD的中点,
∴∠BAC=∠CAD,即∠BAC=∠EAG,
∴cos∠EAG=
2
| ||
| 7 |
在△EAG中,
cos∠EAG=
| AG2+AE2-GE2 |
| 2AG•AE |
∴
| AG2+AE2-GE2 |
| 2AG•AE |
2
| ||
| 7 |
∵AG=
8
| ||
| 3 |
∴
| ||||
2×
|
2
| ||
| 7 |
整理得:GE2=
| 121 |
| 9 |
∵GE>0,∴GE=
| 11 |
| 3 |
∴EG的长为
| 11 |
| 3 |
点评:本题考查了切线的性质、弧与弦的关系、圆周角定理、相似三角形的判定与性质、平行四边形的判定与性质、锐角三角函数的定义、勾股定理、余弦定理等知识,综合性比较强,在△EAG中运用余弦定理是解决本题的关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
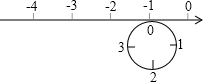 如图,圆的周长为4个单位长度.在该圆的4等分点处分别标上0、1、2、3,先让圆周上表示数字0的点与数轴上表示-1的点重合,再将数轴按逆时针方向环绕在该圆上.则数轴上表示-2014的点与圆周上表示数字几的点重合( )
如图,圆的周长为4个单位长度.在该圆的4等分点处分别标上0、1、2、3,先让圆周上表示数字0的点与数轴上表示-1的点重合,再将数轴按逆时针方向环绕在该圆上.则数轴上表示-2014的点与圆周上表示数字几的点重合( )| A、0 | B、1 | C、2 | D、3 |
下列长度的三条线段能组成三角形的是( )
| A、3,4,6 | ||||
| B、6,9,17 | ||||
| C、5,12,18 | ||||
D、
|
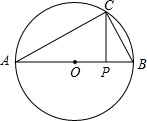 如图所示,在⊙O上有一点C(C不与A、B重合),在直径AB上有一个动点P(P不与A、B重合),试判断PA、PB、PC的大小关系,并说明理由.
如图所示,在⊙O上有一点C(C不与A、B重合),在直径AB上有一个动点P(P不与A、B重合),试判断PA、PB、PC的大小关系,并说明理由. 如图,四边形ABCD,AB+BC=CD+DA,BP平分∠ABM,DP平分∠ADN,求证:∠APB=∠CPD.
如图,四边形ABCD,AB+BC=CD+DA,BP平分∠ABM,DP平分∠ADN,求证:∠APB=∠CPD.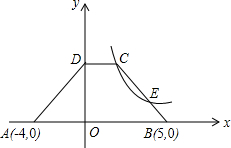 如图,直角坐标内有一个等腰梯形ABCD,DC∥AB,A(-4,0),B(5,0),D在y轴上,C在反比例函数y=
如图,直角坐标内有一个等腰梯形ABCD,DC∥AB,A(-4,0),B(5,0),D在y轴上,C在反比例函数y=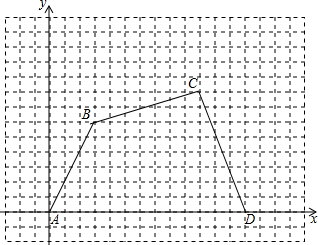 如图,在直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0)、B(3,6)、C(10,8)、D(13,0),确定这个四边形的面积.你是怎样做的?
如图,在直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0)、B(3,6)、C(10,8)、D(13,0),确定这个四边形的面积.你是怎样做的? 如图①,A、B两点同时从原点O出发,点A以每秒m个单位长度沿x轴的正方向运动,点B以每秒n个单位长度沿y轴正方向移动.
如图①,A、B两点同时从原点O出发,点A以每秒m个单位长度沿x轴的正方向运动,点B以每秒n个单位长度沿y轴正方向移动.