题目内容
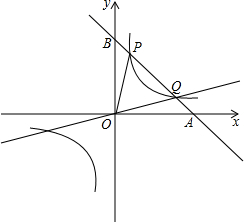
 如图①,A、B两点同时从原点O出发,点A以每秒m个单位长度沿x轴的正方向运动,点B以每秒n个单位长度沿y轴正方向移动.
如图①,A、B两点同时从原点O出发,点A以每秒m个单位长度沿x轴的正方向运动,点B以每秒n个单位长度沿y轴正方向移动.(1)若
| m+2n-5 |
| 2m-n |
(2)如图②,∠ABO和∠BAO的平分线相交于点P,试问:在点A、B运动的过程中,∠P的大小是否会发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
考点:三角形内角和定理,非负数的性质:算术平方根,解二元一次方程组,坐标与图形性质,三角形的外角性质
专题:
分析:(1)根据二次根式的和为0得出关于m、n的方程组,求出m、n的值即可;
(2)求出∠OAB+∠OBA的值,求出∠PAB+∠PBA的值,根据三角形内角和定理求出即可.
(2)求出∠OAB+∠OBA的值,求出∠PAB+∠PBA的值,根据三角形内角和定理求出即可.
解答:解:(1)∵若
+
=0,
∴m+2n-5=0,2m-n=0,
∴m=1,n=2,
∴OA=1,OB=2,
∴A(1,0),B(0,2);
(2)不变,
理由是:∵∠AOB=90°,
∴∠OBA+∠OAB=90°,
∵AP、BP分别平分∠OAB和∠OBA,
∴∠PAB=
∠BAO,∠PBA=
∠OBA,
∴∠PAB+∠PBA=45°,
∴∠APB=180°-45°=135°,
即不发生变化,是135°.
| m+2n-5 |
| 2m-n |
∴m+2n-5=0,2m-n=0,
∴m=1,n=2,
∴OA=1,OB=2,
∴A(1,0),B(0,2);
(2)不变,
理由是:∵∠AOB=90°,
∴∠OBA+∠OAB=90°,
∵AP、BP分别平分∠OAB和∠OBA,
∴∠PAB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠PAB+∠PBA=45°,
∴∠APB=180°-45°=135°,
即不发生变化,是135°.
点评:本题考查了三角形内角和定理,角平分线定义,二次根式的性质,解二次一元方程组的应用,题目比较典型,难度适中.

练习册系列答案
相关题目
计算(-2a2)3÷2a3的结果是( )
| A、-3a3 |
| B、-3a2 |
| C、-4a2 |
| D、-4a3 |
 如图,双曲线y1=
如图,双曲线y1=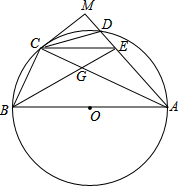 如图:D是以AB为直径的圆O上任意一点,且不与点A、B重合,点C是弧BD的中点,作CE∥AB,交AD或其延长线于E,连接BE交AC与G,AE=CE,过C作CM⊥AD交AD延长线于点M,MC与⊙O相切,CE=7,CD=6,求EG的长.
如图:D是以AB为直径的圆O上任意一点,且不与点A、B重合,点C是弧BD的中点,作CE∥AB,交AD或其延长线于E,连接BE交AC与G,AE=CE,过C作CM⊥AD交AD延长线于点M,MC与⊙O相切,CE=7,CD=6,求EG的长.