题目内容
如图，点D是△ABC的边BC上的点，请问在AC边上是否存在一点E，使△EBD的周长最小？若存在，试作出点E的位置并说明．考点：轴对称-最短路线问题
专题：
分析：根据DB不变，要使△EBD的周长最小，只要求出BE+DE的最小值即可，作D点关于AC的对称点D′，连接D′B，与AC交于点E，E点即为所求．
解答：
解：作点D关于直线AC的对称点D′，连接BD′交AC于点E，则点E为所求．
∵点D关于直线AC的对称点D′，
∴DE=D′E，
∴BE+DE=BE+D′E=BD′，
根据两点之间线段最短，
∴此时△EBD的周长最小．
解：作点D关于直线AC的对称点D′，连接BD′交AC于点E，则点E为所求．∵点D关于直线AC的对称点D′，
∴DE=D′E，
∴BE+DE=BE+D′E=BD′，
根据两点之间线段最短，
∴此时△EBD的周长最小．
点评：此题主要考查了利用轴对称求最短路径的知识，根据已知得出要求△BDE周长的最小值，求出BE+DE的最小值是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列语句是命题的是（ ）
| A、相等的角是对顶角 |
| B、同位角相等吗？ |
| C、国庆60周年大阅兵好壮观呀！ |
| D、过一点作已知直线的垂线 |
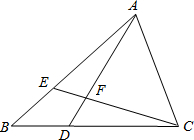如图所示，在△ABC中，点E在AB上，点D在BC上，BD=BE，∠BAD=∠BCE，AD与CE相交于F，试判断AF和CF的数量关系，并说明理由．