题目内容
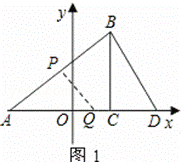
已知:如图,在平面直角坐标系中,△ABC是直角三角形,
∠ACB=90°,点A,C的坐标分别为A(﹣3,0),C(1,0),tan∠BAC= .
.
(1)写出点B的坐标;
(2)在x轴上找一点D,连接BD,使得△ADB与△ABC相似(不包括全等),并
求点D的坐标;
(3)在(2)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,
问是否存在这样的m使得△APQ与△ADB相似?如存在,请求出的m值;
如不存在,请说明理由.

解:(1)B(1,3), (1分)
(2)如图1,过点B作BD⊥AB,交x轴于点D,
在Rt△ABC和Rt△ADB中,
∵∠BAC=∠DAB,
∴Rt△ABC∽Rt△ADB,
∴D点为所求,
又tan∠ADB=tan∠ABC=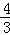 ,
,
∴CD=BC÷tan∠ADB=3÷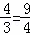 ,
,
∴OD=OC+CD=1+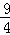 =
=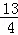 ,
,
∴D( 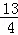 ,0); (4分)
,0); (4分)
(3)这样的m存在.
在Rt△ABC中,由勾股定理得AB=5,
如图1,当PQ∥BD时,△APQ∽△ABD,
则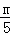 =
= ,
,
解得m=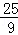 , (6分)
, (6分)
如图2,当PQ⊥AD时,△APQ∽△ADB,
则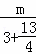 =
=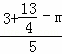 ,
,
解得m=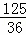 . (9分)
. (9分)
故存在m的值是 或
或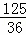 时,使得△APQ与△ADB相似.(10分)
时,使得△APQ与△ADB相似.(10分)
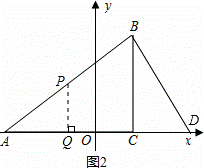

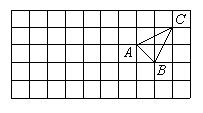
根据下面给出的数轴,解答下面的问题:(本题6分)
 |
⑴ 请你根据图中A、B两点的位置,分别写出它们所表示的有理数A: B: ;
⑵ 观察数轴,与点A的距离为4的点表示的数是: ;
⑶ 若将数轴折叠,使得A点与-3表示的点重合,则B点与数 表示的 点重合;
点重合;
⑷ 若数轴上M、N两点之间的距离为2014(M 在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M: N: .
在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M: N: .



 的根,则三角形的
的根,则三角形的 周长为( )
周长为( ) ( )
( ) D. 6
D. 6
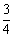 ,求DC的长.
,求DC的长. 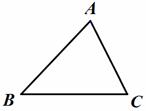
 +
+ ≥
≥ 恒成立,则n的最大值为 .
恒成立,则n的最大值为 .