题目内容
15.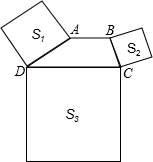 如图,在梯形ABCD中,AB∥DC,∠ADC+∠BCD=90°,且DC=2AB,分别以DA、BC、DC为边向梯形外作正方形,其面积分别为S1=7,S2=4,则S3的面积是44.
如图,在梯形ABCD中,AB∥DC,∠ADC+∠BCD=90°,且DC=2AB,分别以DA、BC、DC为边向梯形外作正方形,其面积分别为S1=7,S2=4,则S3的面积是44.
分析 延长DA、CB交于点E,由正方形的性质得出AD=$\sqrt{7}$,BC=2,由平行线得出△ABE∽△DCE,得出对应边成比例$\frac{AE}{DE}=\frac{BE}{CE}=\frac{AB}{CD}$,得出DE=2AE=2AD=2$\sqrt{7}$,CE=2BE=2BC=4,证出∠E=90°,由勾股定理求出CD2即可.
解答 解:延长DA、CB交于点E,如图所示: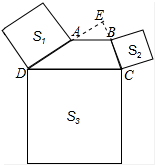
∵S1=7,S2=4,
∴AD=$\sqrt{7}$,BC=2,
∵AB∥CD,
∴△ABE∽△DCE,
∴$\frac{AE}{DE}=\frac{BE}{CE}=\frac{AB}{CD}$,
∵DC=2AB,
∴$\frac{AE}{DE}=\frac{BE}{CE}$=$\frac{1}{2}$,
∴DE=2AE=2AD=2$\sqrt{7}$,CE=2BE=2BC=4,
∵∠ADC+∠BCD=90°,
∴∠E=90°,
∴CD2=DE2+CE2=(2$\sqrt{7}$)2+42=44,
∴S=44;
故答案为:44.
点评 本题考查了正方形的性质、平行线的性质、相似三角形的判定与性质、勾股定理、直角三角形的判定等知识;本题综合性强,证明三角形相似和运用勾股定理是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.计算$\sqrt{8}$-$\sqrt{2}$,正确的结果是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{4}$ | C. | $\sqrt{6}$ | D. | 3$\sqrt{2}$ |
3.下列函数,当x>0时,y随x的增大而增大的是( )
| A. | y=-2x | B. | y=$\frac{2}{x}$ | C. | y=2x-1 | D. | y=-x2+1 |
20.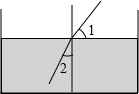 如图,当光线从空气射入水中时,光线的传播方向发生了改变,这就是折射现象.图中∠1=47°,∠2=30°,则光的传播方向改变的度数为( )
如图,当光线从空气射入水中时,光线的传播方向发生了改变,这就是折射现象.图中∠1=47°,∠2=30°,则光的传播方向改变的度数为( )
 如图,当光线从空气射入水中时,光线的传播方向发生了改变,这就是折射现象.图中∠1=47°,∠2=30°,则光的传播方向改变的度数为( )
如图,当光线从空气射入水中时,光线的传播方向发生了改变,这就是折射现象.图中∠1=47°,∠2=30°,则光的传播方向改变的度数为( )| A. | 13° | B. | 15° | C. | 17° | D. | 19° |
4.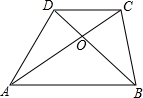 如图,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O,有下面四个结论:①△AOB∽△COD;②△AOD∽△BOC;③S△AOD=S△BOC;④S△DOC:S△BOA=DC:AB,其中,结论一定正确的有( )
如图,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O,有下面四个结论:①△AOB∽△COD;②△AOD∽△BOC;③S△AOD=S△BOC;④S△DOC:S△BOA=DC:AB,其中,结论一定正确的有( )
 如图,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O,有下面四个结论:①△AOB∽△COD;②△AOD∽△BOC;③S△AOD=S△BOC;④S△DOC:S△BOA=DC:AB,其中,结论一定正确的有( )
如图,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O,有下面四个结论:①△AOB∽△COD;②△AOD∽△BOC;③S△AOD=S△BOC;④S△DOC:S△BOA=DC:AB,其中,结论一定正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.若$\sqrt{(a-b)^{2}}$=b-a,则( )
| A. | a>b | B. | a<b | C. | a≥b | D. | a≤b |
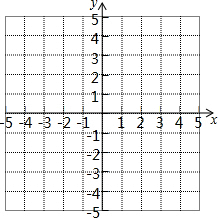 如图,描出A(-3,-2)、B(2,-2)、C(-2,1)、D(3,1)四个点,线段AB、CD有什么关系?顺次连接A、B、C、D四点组成的图形是什么图形?
如图,描出A(-3,-2)、B(2,-2)、C(-2,1)、D(3,1)四个点,线段AB、CD有什么关系?顺次连接A、B、C、D四点组成的图形是什么图形?