题目内容
1.⊙O是△ABC的外接圆,AB是直径,过$\widehat{BC}$的中点P作⊙O的直径PG交弦BC于点D,连接AG,CP,PB.
(1)如题图1;若D是线段OP的中点,求∠BAC的度数;
(2)如题图2,在DG上取一点k,使DK=DP,连接CK,求证:四边形AGKC是平行四边形;
(3)如题图3,取CP的中点E,连接ED并延长ED交AB于点H,连接PH,求证:PH⊥AB.
分析 (1)如图1,根据垂径定理得到PG⊥BC,则BD垂直平分OP,于是可判断△OBP为等边三角形,所以∠BOP=60°,然后估计圆周角定理得到∠BAC=∠BOP=60°;
(2)连接KB,GB、PA,如图2,先判定四边形BPCK为平行四边形得到PB=CK,PB∥CK,再判断四边形APBG为平行四边形得到PB=AG,PB∥AG,则CK=AG,CK∥AG然后判断四边形AGCK是平行四边形;
(3)如图3,先估计三角形中位线性质得DE∥PB,即DH∥PB,再判定△ODH为等腰三角形得到OD=OH,接着证明△OBD≌△HOP,则∠OHP=∠ODB=90°.所以PH⊥AB.
解答 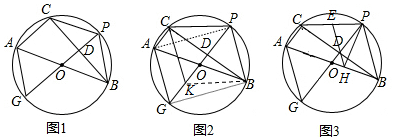 (1)解:如图1,
(1)解:如图1,
∵AB为⊙O直径,点P是$\widehat{BC}$的中点,
∴PG⊥BC,即∠ODB=90°.
∵D为OP的中点,
∴BD垂直平分OP,
∴BP=BO,
而OB=OP,
∴△OBP为等边三角形,
∴∠BOP=60°,
∴∠BAC=∠BOP=60°;
(2)证明:连接KB,GB、PA,如图2,
由(1)知,CD=BD,
∵DK=DP,
∴四边形BPCK为平行四边形,
∴PB=CK,PB∥CK,
∵PA=OB,OG=OP,
∴四边形APBG为平行四边形,
∴PB=AG,PB∥AG,
∴CK=AG,CK∥AG,
∴四边形AGCK是平行四边形;
(3)证明:如图3,
∵CE=PE,CD=BD,
∴DE∥PB,即DH∥PB,
而△OPB为等腰三角形,
∴△ODH为等腰三角形,
∴OD=OH,
在△ODB和△OHP中
$\left\{\begin{array}{l}{OD=OH}\\{∠BOD=∠POH}\\{OB=OP}\end{array}\right.$,
∴△OBD≌△HOP(SAS),
∴∠OHP=∠ODB,
而BC⊥DG,
∴∠OHP=∠ODB=90°.
∴PH⊥AB.
点评 本题考查了圆的综合题:熟练掌握垂径定理、圆周角定理和等边三角形的判定与性质;灵活应用平行四边形的判定与性质;会应用全等三角形的知识解决角相等的问题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | x≠-$\frac{1}{2}$ | B. | x>$\frac{1}{2}$ | C. | x>-$\frac{1}{2}$ | D. | x≥-$\frac{1}{2}$ |
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
| 运输工具 | 途中平均速度 (千米/时) | 运费 (元/千米) | 装卸费用 (元) |
| 火车 | 100 | 15 | 2000 |
| 汽车 | 80 | 20 | 900 |
(2)你若是该市水果批发部门的经理,要想将这种水果运往本市销售,你将选择哪种运输方式比较合算呢?
 如图,直线AB和EF相交于O,OC平分∠AOB,∠COE=65°,试求∠FOB的度数.
如图,直线AB和EF相交于O,OC平分∠AOB,∠COE=65°,试求∠FOB的度数.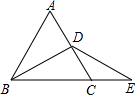 如图,等边△ABC的周长是12,D是AC边上的中点,E在BC的延长线上,若DE=DB,则CE的长为2.
如图,等边△ABC的周长是12,D是AC边上的中点,E在BC的延长线上,若DE=DB,则CE的长为2.