题目内容
4．⊙O中，弧AB的长度为弧MN的2倍，则下列关于弦的结论正确的是（ ）| A． | AB＞2MN | B． | AB=2MN | ||
| C． | AB＜2MN | D． | AB与2MN的大小不能确定 |
分析 如图，取$\widehat{AB}$的中点C，连接AC，BC，根据已知条件得到$\widehat{AC}$=$\widehat{BC}$=$\widehat{MN}$，得到AC=BC=MN，根据三角形的三边关系即可得到结论．
解答 
解：如图，取$\widehat{AB}$的中点C，连接AC，BC，
∴$\widehat{AC}$=$\widehat{BC}$=$\frac{1}{2}$$\widehat{AB}$，
∵$\widehat{MN}$=$\frac{1}{2}$$\widehat{AB}$，
∴$\widehat{AC}$=$\widehat{BC}$=$\widehat{MN}$，
∴AC=BC=MN，
∵AB＜AC+BC，
∴AB＜2MN，
故选C．
点评 本题考查了弧、弦、圆心角的关系，三角形的三边关系，正确的理解题意是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
9．
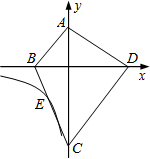如图，四边形ABCD的顶点都在坐标轴上，若AB∥CD，△ABD与△ACD的面积分别为20和30，若双曲线y=$\frac{k}{x}$恰好经过BC的中点E，则k的值为（ ）
如图，四边形ABCD的顶点都在坐标轴上，若AB∥CD，△ABD与△ACD的面积分别为20和30，若双曲线y=$\frac{k}{x}$恰好经过BC的中点E，则k的值为（ ）| A． | 3 | B． | -3 | C． | -6 | D． | 6 |
16．
如图，沿对角线AC折叠正方形ABCD，使得B、D重合，再折叠△ACD，点D恰好落在AC上的点E处，测得折痕AF的长为3，则C到AF的距离CG为（ ）
如图，沿对角线AC折叠正方形ABCD，使得B、D重合，再折叠△ACD，点D恰好落在AC上的点E处，测得折痕AF的长为3，则C到AF的距离CG为（ ）| A． | $\frac{3}{2}$ | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $\sqrt{5}$-1 |