题目内容
3. 如图所示,正方形ABCD的边长为4cm,E,F分别是BC,DC边上的动点,E,F同时从点C以1cm/s的速度分别向点B、点D移动,当点E与点B重合时,运动停止,设运动时间为x(s),运动过程中△AEF的面积为y.
如图所示,正方形ABCD的边长为4cm,E,F分别是BC,DC边上的动点,E,F同时从点C以1cm/s的速度分别向点B、点D移动,当点E与点B重合时,运动停止,设运动时间为x(s),运动过程中△AEF的面积为y.(1)写出y与x之间的函数表达式,并求出自变量x的取值范围.
(2)比较当x=2和x=3时,△AEF的面积的大小.
分析 (1)根据△AEF的面积=正方形ABCD的面积-△ABE的面积-△ADF的面积-△ECF的面积,分别表示正方形ABCD的面积、△ABE的面积、△ADF的面积、△ECF的面积代入即可;
(2)把当x=2和x=3分别代入(1)中的函数关系式即可求出△AEF的面积的大小.
解答 解:(1)设运动时间为x(s),
∵点E,F同时从点C出发,以每秒1cm的速度分别向点B,D运动,
∴CE=x,CF=x,BE=4-x,DF=4-x,
∴△AEF的面积=正方形ABCD的面积-△ABE的面积-△ADF的面积-△ECF的面积,
即:y=16-$\frac{1}{2}$AB•AE-$\frac{1}{2}$AD•DF-$\frac{1}{2}$EC•FC,
=16-$\frac{1}{2}$×4×(4-x)-$\frac{1}{2}$×4×(4-x)-$\frac{1}{2}$•x•x,
=-$\frac{1}{2}$x2+4x.(0≤x≤2);
(2)当x=2时,△AEF的面积=-$\frac{1}{2}$×4+8=6;
当x=3时,△AEF的面积=-$\frac{1}{2}$×9+12=7.5.
点评 此题考查了函数关系式,解题关键是正确表示正方形ABCD的面积、△ABE的面积、△ADF的面积、△ECF的面积.

练习册系列答案
相关题目
18.分式$\frac{1}{{a}^{2}-{b}^{2}}$和$\frac{1}{a+b}$的最简公分母是( )
| A. | a+b | B. | a-b | C. | a2-b2 | D. | a2+b2 |
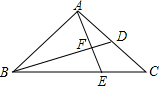 如图,△ABC中,BD平分∠ABC,点E是BC上一点,且满足AB2=BE•BC,AE与BD相交于点F.
如图,△ABC中,BD平分∠ABC,点E是BC上一点,且满足AB2=BE•BC,AE与BD相交于点F. 如图,△ABC中,D为AB边上一点,已知AB=AC,AD=CD=BC,求△ABC中的各角的度数.
如图,△ABC中,D为AB边上一点,已知AB=AC,AD=CD=BC,求△ABC中的各角的度数.