题目内容
17.已知关于x的一元二次方程(x+1)2=m有两个不等实数根,则m的取值范围是( )| A. | m≥-1 | B. | m>0 | C. | m≥1 | D. | m≥0 |
分析 首先把方程转化为一元二次方程的一般形式,然后求得b2-4ac的值,再进一步根据一元二次方程(x+1)2=m有两个不等实数根,即△>0进行求解.
解答 解:∵(x+1)2=m,
∴x2+2x+1-m=0,
∵关于x的一元二次方程(x+1)2=m有两个不等实数根,
∴b2-4ac=4-4+4m>0,
即m>0.
故选B.
点评 此题考查了一元二次方程的根的判别式,能够根据一元二次方程的根的判别式和方程的根的情况求得字母的取值范围.

练习册系列答案
相关题目
7.下表是某服装店的原价表,国庆期间该店优惠大酬宾,外套按原价打六折出售,衬衫和裤子按原价打八折出售,已知这三种服饰共卖出200件,共得33860元.设外套卖出x件,由题意可得方程( )
| 服饰 | 原价(元) |
| 外套 | 299 |
| 衬衫 | 199 |
| 裤子 | 199 |
| A. | 0.8×199x+0.6×299(200+x)=33860 | B. | 0.8×199x+0.6×299(200-x)=33860 | ||
| C. | 0.6×299x+0.8×199(200+x)=33860 | D. | 0.6×299x+08×199(200-x)=33860 |
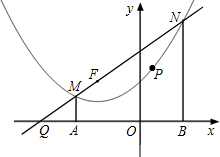 如图,过点F(-2,2)的直线l与抛物线y=$\frac{1}{4}$x2+x+2交于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.
如图,过点F(-2,2)的直线l与抛物线y=$\frac{1}{4}$x2+x+2交于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.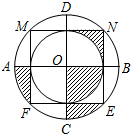 如图,边长为2的正方形MNEF的四个顶点在大圆O上,小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,则图中阴影部分的面积是$\frac{1}{2}$π.
如图,边长为2的正方形MNEF的四个顶点在大圆O上,小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,则图中阴影部分的面积是$\frac{1}{2}$π.
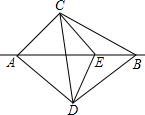 如图,AC=AD,∠CAB=∠DAB,E是直线AB上一个动点,连接EC,ED,问EC与ED,∠CEA与∠DEA之间有什么关系?就E点的不同位置加以证明.
如图,AC=AD,∠CAB=∠DAB,E是直线AB上一个动点,连接EC,ED,问EC与ED,∠CEA与∠DEA之间有什么关系?就E点的不同位置加以证明.