题目内容
 如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.(1)求证:四边形ABFC为平行四边形;
(2)请你探索EC和AD的关系,并说明理由.
考点:平行四边形的判定与性质
专题:
分析:(1)根据平行四边形性质得出AB∥CD,推出AE=EF,根据平行四边形的判定得出四边形ABFC是平行四边形;
(2)利用三角形中位线定理进行判断.
(2)利用三角形中位线定理进行判断.
解答:(1)证明:∵E为BC中点,
∴BE=EC,
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴△ABE∽△FCE,
∴
=
,
∴AE=EF,
∵NE=EC,
∴四边形ABFC是平行四边形;
(2)解:∵由(1)知,四边形ABFC是平行四边形,
∴AE=EF.
又∵EC∥AD,
∴EC是△AFD的中位线,
∴EC=
AD.
综上所述,EC∥AD,且EC=
AD.

∴BE=EC,
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴△ABE∽△FCE,
∴
| AE |
| EF |
| BE |
| EC |
∴AE=EF,
∵NE=EC,
∴四边形ABFC是平行四边形;
(2)解:∵由(1)知,四边形ABFC是平行四边形,
∴AE=EF.
又∵EC∥AD,
∴EC是△AFD的中位线,
∴EC=
| 1 |
| 2 |
综上所述,EC∥AD,且EC=
| 1 |
| 2 |
点评:本题考查了平行四边形的性质和判定的应用,注意:①平行四边形的对边互相平行且相等;②对角线互相平分的四边形是平行四边形.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
 由于被墨水污染,一道几何题仅能见到如图所示的图形和文字:
由于被墨水污染,一道几何题仅能见到如图所示的图形和文字: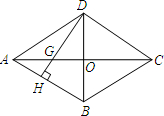 如图,四边形ABCD是菱形,对角线AC与BD交于点O,AD=BD=6cm,DH⊥AB于点H,且DH与AC交于G,则GH的长度为
如图,四边形ABCD是菱形,对角线AC与BD交于点O,AD=BD=6cm,DH⊥AB于点H,且DH与AC交于G,则GH的长度为