题目内容
 如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE.求证:
如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE.求证:(1)△ABC≌△ADE;
(2)AB=AD.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)首先根据三角形内角和定理可得∠E=∠C,再根据等式的性质可得∠BAC=∠DAE,然后再利用ASA定理证明△ABC≌△ADE;
(2)利用全等三角形对应边相等可得AB=AD.
(2)利用全等三角形对应边相等可得AB=AD.
解答:证明:(1)∵∠2=∠3,∠AFE=∠CFD,
∴∠E=∠C.
∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠DAE.
在△ABC和△ADE中,
,
∴△ABC≌△ADE(SAS);
(2)∵△ABC≌△ADE,
∴AD=AE.
∴∠E=∠C.
∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠DAE.
在△ABC和△ADE中,
|
∴△ABC≌△ADE(SAS);
(2)∵△ABC≌△ADE,
∴AD=AE.
点评:此题主要考查了全等三角形的判定与性质,关键是掌握全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
某商店出售两件衣服,每件60元,其中一件赚25%,而另一件赔25%,那么这家商店( )
| A、赚了 | B、赔了 |
| C、不赚也不赔 | D、不能确定 |


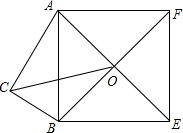 Rt△ABC中,∠C=90°,AC=3,BC=5,以AB为一边向外作正方形ABDF,O为AE、BF交点,则OC长为
Rt△ABC中,∠C=90°,AC=3,BC=5,以AB为一边向外作正方形ABDF,O为AE、BF交点,则OC长为 如图,等边△ABC中,点M是BC上一点,点N是CA上一点,且BM=CN,AM与BN相交于Q点.
如图,等边△ABC中,点M是BC上一点,点N是CA上一点,且BM=CN,AM与BN相交于Q点. 实数a、b在数轴上的位置如图所示,化简:
实数a、b在数轴上的位置如图所示,化简: 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第2010个正方形的面积为
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第2010个正方形的面积为