题目内容
14.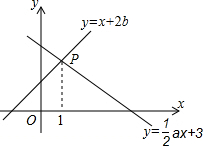 如图,已知函数y=x+2b和y=$\frac{1}{2}$ax+3的图象交于点P,则不等式x+2b>$\frac{1}{2}$ax+3的解集为x>1.
如图,已知函数y=x+2b和y=$\frac{1}{2}$ax+3的图象交于点P,则不等式x+2b>$\frac{1}{2}$ax+3的解集为x>1.
分析 根据一次函数的图象和两函数的交点坐标即可得出答案.
解答 解:由图知:当直线y=x+2b的图象在直线y=$\frac{1}{2}$ax+3的上方时,不等式x+2b>$\frac{1}{2}$ax+3成立;
由于两直线的交点横坐标为:x=1,
观察图象可知,当x>1时,x+2b>$\frac{1}{2}$ax+3;
故答案为:x>1.
点评 此题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
19.以下各式计算正确的是( )
| A. | (y+x)(-y+x)=y2-x2 | B. | -$\root{3}{-{2}^{-3}}$=-2 | C. | (-2a2)3=-8a6 | D. | x6÷x3=x2 |
3.64的算术平方根是( )
| A. | 4 | B. | ±4 | C. | 8 | D. | ±8 |
 在图中画出△ABC平移的图象,使点A移到点A′.
在图中画出△ABC平移的图象,使点A移到点A′.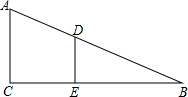 身高1.5m的某同学沿平直路线匀速行走,路灯在行进路线的正上方某一高度,某时刻人影的长度为0.6m,前进4m后,影长变为1.4m,求路灯的高度.(提示:如图所示的两直角三角形ACB、DEB的边长之间存在如下关系:$\frac{AC}{DE}$=$\frac{BC}{BE}$)
身高1.5m的某同学沿平直路线匀速行走,路灯在行进路线的正上方某一高度,某时刻人影的长度为0.6m,前进4m后,影长变为1.4m,求路灯的高度.(提示:如图所示的两直角三角形ACB、DEB的边长之间存在如下关系:$\frac{AC}{DE}$=$\frac{BC}{BE}$)