题目内容
在等腰三角形ABC中,AO⊥BC于点O,AB=AC=6,∠ABC=30°,以BC所在的直线为x轴,以AO所在的直线为y轴,建立平面直角坐标系,将与△ABC重合的△DEF(点D与点A、点E与点B、点F与点C分别重合)沿x轴向右平移,当点E与点O重合时,停止移动,然后将△DEF绕点O逆时针旋转,当ED与y轴的正半轴重合时,停止转动(如图1).
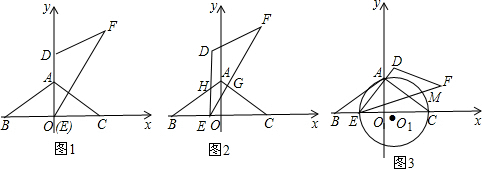
(1)F点的坐标为:( , ).
(2)将△DEF沿x轴向左平移,当点E与点B重合时,停止移动,在移动过程中,ED与AB相交于点H,EF与CA的延长线相交于点G(如图2所示),设BE=m,以A、H、E、G为顶点的四边形面积为S,求S与m之间的函数关系式;
(3)如图3,△DEF的顶点E在△ABC的BC边上移动,ED经过点A,过A、E、C三点作⊙O1交EF于点M,连结CM.
①当⊙O1与AB相切时,求⊙O1的半径.
②设点M的坐标为(x,y),请求出y与x之间的函数关系式.

(1)F点的坐标为:(
(2)将△DEF沿x轴向左平移,当点E与点B重合时,停止移动,在移动过程中,ED与AB相交于点H,EF与CA的延长线相交于点G(如图2所示),设BE=m,以A、H、E、G为顶点的四边形面积为S,求S与m之间的函数关系式;
(3)如图3,△DEF的顶点E在△ABC的BC边上移动,ED经过点A,过A、E、C三点作⊙O1交EF于点M,连结CM.
①当⊙O1与AB相切时,求⊙O1的半径.
②设点M的坐标为(x,y),请求出y与x之间的函数关系式.
考点:圆的综合题
专题:
分析:(1)根据全等三角形的性质,可得对应角相等,对应边相等,根据锐角三角函数中的正弦、余弦,可得答案;
(2)根据等腰三角形的三线合一,可得直角三角形,根据勾股定理,可得OA的长、BO的长,EH的长,根据两锐角互余,可得三角形是直角三角形,根据锐角三角函数,可得CG的长,分类讨论:当2
<m<3
时,根据面积的差,可得答案;当0<m<2
时,根据面积的和,可得答案;
(3)①根据垂径定理,可得AR的长,根据切线的性质,可得∠BAO1的度数,根据与弦函数,可得答案;②根据同弧所对的圆周角,可得∠AEM与∠MCA的关系,根据正切函数,可得答案.
(2)根据等腰三角形的三线合一,可得直角三角形,根据勾股定理,可得OA的长、BO的长,EH的长,根据两锐角互余,可得三角形是直角三角形,根据锐角三角函数,可得CG的长,分类讨论:当2
| 3 |
| 3 |
| 3 |
(3)①根据垂径定理,可得AR的长,根据切线的性质,可得∠BAO1的度数,根据与弦函数,可得答案;②根据同弧所对的圆周角,可得∠AEM与∠MCA的关系,根据正切函数,可得答案.
解答:解:(1)作EG⊥BC与G点,如图中的图1:

在等腰三角形ABC中,AO⊥BC于点O,AB=AC=6,∠ABC=30°,
∴OA=3,OC=BO=3
,BC=6
,
∵△ABC≌△DEF,
∴∠DOF=30°,EF=BG=6
,
∠EOG=60,
EG=EFcos∠FOG═6
×
=3
,
FG=EFsin∠FOG=6
×
=9,
∴F点的坐标为(3
,9),
故答案为:(3
,9);
(2)在△ABC中,∵AB=AC=6,∠ABC=30°,
∴OA=3,OC=BO=3
,BC=6
,∠ACB=∠ABC=30°,∠BAC=120°.
∵HE⊥BC,∠ABC=30°,BE=m,∴EH=
m.
∵∠DEF=∠ACB=30°,
∴∠GEC=60°,∠C=30°,
∴∠EGC=90°.
∴在Rt△EGC中,
EC=6
-m,EG=
EC=
,CG=ECcos30°=
.
①当2
<m<3
时,S四边形AHEG=S△ABC-S△BEH-S△EGC
=
BC•OA-
BE•EH-
EG•CG=
×6
×3-
m•
m-
•
•
即S四边形AHEG=-
m2+
m-
.②当0<m<2
时,
如图中的图1,过H点作HQ⊥GE,垂足为Q,

则 HQ=
EH=
m,
AG=CG-AC=
-6.
S四边形AGHE=S△HEG+S△GEA
=
EG•HQ+
EG•AG
=
×
×
+
×
×[
-6]
即S四边形AGHE=
m2-
m+
;
(3)①如图中的图3,连接O1A和O1C,过点O1作O1R⊥AC,垂足为R,

∴O1A=O1C,AR=
AC=
×6=3.
当AB与⊙O1相切时,∠BAO1=90°
∴∠O1AC=120°-90°=30°.
∴cos∠O1AC=cos30°=
=
∴O1A=2
,
即⊙O1的半径是2
;
②如图,过点M作MH⊥BC于点H,
∴OH=x,MH=y.
∵
=
,
∴∠AEM=∠MCA=30°.
∵∠ACB=30°,
∴∠MCH=60°
∴tan∠MCH=tan60°=
=
=
,
∴y=-
x+9.

在等腰三角形ABC中,AO⊥BC于点O,AB=AC=6,∠ABC=30°,
∴OA=3,OC=BO=3
| 3 |
| 3 |
∵△ABC≌△DEF,
∴∠DOF=30°,EF=BG=6
| 3 |
∠EOG=60,
EG=EFcos∠FOG═6
| 3 |
| 1 |
| 2 |
| 3 |
FG=EFsin∠FOG=6
| 3 |
| ||
| 2 |
∴F点的坐标为(3
| 3 |
故答案为:(3
| 3 |
(2)在△ABC中,∵AB=AC=6,∠ABC=30°,
∴OA=3,OC=BO=3
| 3 |
| 3 |
∵HE⊥BC,∠ABC=30°,BE=m,∴EH=
| ||
| 3 |
∵∠DEF=∠ACB=30°,
∴∠GEC=60°,∠C=30°,
∴∠EGC=90°.
∴在Rt△EGC中,
EC=6
| 3 |
| 1 |
| 2 |
6
| ||
| 2 |
| ||||
| 2 |
①当2
| 3 |
| 3 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 3 |
| 1 |
| 2 |
6
| ||
| 2 |
| ||||
| 2 |
即S四边形AHEG=-
7
| ||
| 24 |
| 9 |
| 2 |
9
| ||
| 2 |
| 3 |
如图中的图1,过H点作HQ⊥GE,垂足为Q,

则 HQ=
| 1 |
| 2 |
| ||
| 6 |
AG=CG-AC=
| ||||
| 2 |
S四边形AGHE=S△HEG+S△GEA
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
6
| ||
| 2 |
| ||
| 6 |
| 1 |
| 2 |
6
| ||
| 2 |
| ||||
| 2 |
即S四边形AGHE=
| ||
| 12 |
| 9 |
| 4 |
9
| ||
| 2 |
(3)①如图中的图3,连接O1A和O1C,过点O1作O1R⊥AC,垂足为R,

∴O1A=O1C,AR=
| 1 |
| 2 |
| 1 |
| 2 |
当AB与⊙O1相切时,∠BAO1=90°
∴∠O1AC=120°-90°=30°.
∴cos∠O1AC=cos30°=
| AR |
| O1A |
| 3 |
| O1A |
∴O1A=2
| 3 |
即⊙O1的半径是2
| 3 |
②如图,过点M作MH⊥BC于点H,
∴OH=x,MH=y.
∵
 |
| AM |
 |
| AM |
∴∠AEM=∠MCA=30°.
∵∠ACB=30°,
∴∠MCH=60°
∴tan∠MCH=tan60°=
| MH |
| HC |
| y |
| OC-OH |
| 3 |
| y | ||
3
|
∴y=-
| 3 |
点评:本题考查了圆的综合题,利用了垂径定理,切线的性质,同弧所对的圆周角相等,锐角三角函数,题目稍有难度.

练习册系列答案
相关题目
如图,每个图形都由同样大小的矩形按照一定的规律组成,其中第①个图形的面积为6cm2,第②个图形的面积为18cm2,第③个图形的面积为36cm2,…,那么第⑥个图形的面积为( )
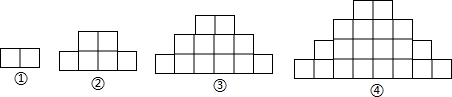

| A、84cm2 |
| B、90cm2 |
| C、126cm2 |
| D、168cm2 |
 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形.请在图中方格纸中,按要求完成下列各题:
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形.请在图中方格纸中,按要求完成下列各题: 如图,A市在B市的北偏东60°方向,在C市的西北方向,D市在B市的正南方向.已知A、B两市相距120km,B、D两市相距100km..问:A市与C、D两市分别相距多少千米?(结果精确到1km)
如图,A市在B市的北偏东60°方向,在C市的西北方向,D市在B市的正南方向.已知A、B两市相距120km,B、D两市相距100km..问:A市与C、D两市分别相距多少千米?(结果精确到1km)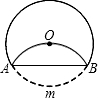 如图,⊙O的半径为6,将圆沿AB折叠后,圆弧恰好经过圆心,则弧AmB的长度为
如图,⊙O的半径为6,将圆沿AB折叠后,圆弧恰好经过圆心,则弧AmB的长度为