题目内容
9.已知直线l1:y=-4x+5,l2:y=$\frac{1}{2}$x-4,求这两条直线的交点坐标,并判断该交点落在哪个象限内.分析 由两直线的方程,即可联立起来求出两直线的交点坐标,进而可判断出交点所在的象限.
解答 解:联立两直线的方程$\left\{\begin{array}{l}{y=-4x+5}\\{y=\frac{1}{2}x-4}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$,
∴两条直线l1和l2的交点坐标为(2,-3),
∵x=2>0,y=-3<0,
∴该交点落在平面直角坐标系的第四象限.
点评 本题主要考查了函数图象交点坐标的求法,充分理解一次函数与方程组的联系是解答此类问题的关键.

练习册系列答案
相关题目
19.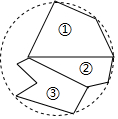 小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
 小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )| A. | ① | B. | ② | C. | ③ | D. | 均不可能 |
 如图,BD=DE=EC,则线段AE是△ADC的中线.
如图,BD=DE=EC,则线段AE是△ADC的中线.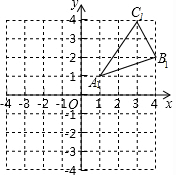 如图,△A1B1C1是由△ABC经过平移后得到的,且顶点A1的坐标A1(1,1).
如图,△A1B1C1是由△ABC经过平移后得到的,且顶点A1的坐标A1(1,1).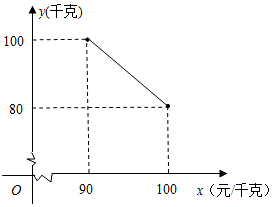 某茶叶专卖店经销一种日照绿茶,每千克成本80元,据销售人员调查发现,每月的销售量y(千克)与销售单价x(元/千克)之间存在如图所示的变化规律.
某茶叶专卖店经销一种日照绿茶,每千克成本80元,据销售人员调查发现,每月的销售量y(千克)与销售单价x(元/千克)之间存在如图所示的变化规律.