题目内容
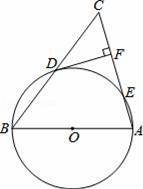
如图,△ABC的内角∠ABC与外角∠ACD的平分线交于点E,且CE∥AB,AC与BE交于点E,则下列结论错误的是( )


A.CB=CE B.∠A=∠ECD C.∠A=2∠E D.AB=BF
D【考点】三角形内角和定理;平行线的性质.
【分析】选项A和B:根据角平分线定义和平行线的性质推出∠FBC=∠E即可;选项C:先根据三角形外角的性质及角平分线的定义得出∠ACD=∠A+∠ABC,∠ECD=
 ∠ACD=
∠ACD=
 (∠A+∠ABC),再由BE平分∠ABC可知∠EBC=
(∠A+∠ABC),再由BE平分∠ABC可知∠EBC=
 ∠ABC,根据∠ECD是△BCE的外角即可得出结论;选项D:根据等腰三角形的判定和已知推出即可.
∠ABC,根据∠ECD是△BCE的外角即可得出结论;选项D:根据等腰三角形的判定和已知推出即可.
【解答】解:∵△ABC的内角∠ABC与外角∠ACD的平分线交于点E,
∴∠ABF=∠CBF,∠FCE=∠ECD,
∵CE∥AB,
∴∠A=∠FCE,∠E=∠ABE,
∴∠A=∠ECD,∠FBC=∠E,
∴CB=CE,
∵∠ACD=∠A+∠ABC,CE平分∠ACD,
∴∠ECD=
 ∠ACD=
∠ACD=
 (∠A+∠ABC)(角平分线的定义),
(∠A+∠ABC)(角平分线的定义),
∵BE平分∠ABC,
∴∠EBC=
 ∠ABC(角平分线的定义),
∠ABC(角平分线的定义),
∵∠ECD是△BCE的外角,
∴∠E=∠ECD﹣∠EBC=
 ∠A,
∠A,
即∠A=2∠E;
根据已知条件不能推出∠A=∠AFB,即不能推出AB=BF;
所以选项A、B、C的结论都正确,只有选项D的结论错误;
故选D.
【点评】本题考查的是三角形外角的性质,平行线的性质,等腰三角形的判定的应用,能综合运用知识点进行推理是解此题的关键.

练习册系列答案
相关题目
 ABCD中,点E在AB上,线段CE,BD相交于点F,若AE:BE=4:3,且
ABCD中,点E在AB上,线段CE,BD相交于点F,若AE:BE=4:3,且 F=2.则DF=
F=2.则DF= 

 +
+

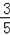
 ,CF=9,求AE的长.
,CF=9,求AE的长.