��Ŀ����
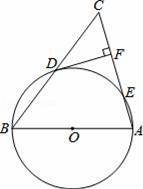
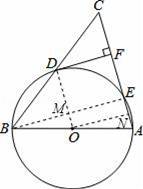
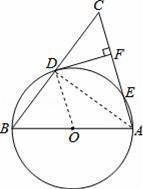
ij��Ϊ����ǿѧ�����ʣ�ȫ��ʵʩ��ѧ�������̡�Ӫ�����̣�ijƷ��ţ�̹�Ӧ���ṩ��ԭζ����ݮζ������ζ�����ζ������ζ���ֿ�ζ��ţ���ṩѧ�����ã������ѧΪ���˽�ѧ���Բ�ͬ��ζţ�̵�ϲ�ã���ȫУ����ţ�̵�ѧ��������������飨2014•������һģ����ͼ���ڡ�ABC�У�AB=AC����ABΪֱ���ġ�O���BC��AC�ֱ���D��E���㣬DF��AC��F��
��1����֤��DFΪ��O�����ߣ�
��2����cosC=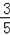
 ��CF=9����AE�ij���
��CF=9����AE�ij���

��
�����㡿���ߵ��ж���
����������1������OD��AD�����OD��AC���Ƴ�OD��DF���������ߵ��ж��Ƴ����ɣ�
��2�����CD��DF���Ƴ��ı���DMEF���ı���OMEN�Ǿ��Σ��Ƴ�OM=EN��EM=DF=12�����OM����������𰸣�
����𡿽⣺��1������OD��AD��
��AB�ǡѵ�ֱ����
���ADB=90�㣬
�֡�AB=AC��
��BD=CD
�֡�OB=OA��
��OD��AC
��DF��AC��
��OD��DF
�֡�ODΪ�ѵİ뾶��
��DFΪ��O�����ߣ�
��2������BE��OD��M����O��ON��AE��N��
��AE=2NE��
��cosC=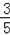
 ��CF=9��
��CF=9��
��DC=15��
��DF=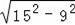
 =12��
=12��
��AB��ֱ����
���AEB=��CEB=90�㣬
��DF��AC��OD��DF��
���DFE=��FEM=��MDF=90�㣬
���ı���DMEF�Ǿ��Σ�
��EM=DF=12����DME=90�㣬DM=EF��
��OD��BE��
ͬ���ı���OMEN�Ǿ��Σ�
��OM=EN��
��ODΪ�뾶��
��BE=2EM=24��
�ߡ�BEA=��DFC=90�㣬��C=��C��
���CFD�ס�CEB��
��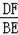
 =
=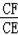
 ��
��
��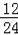
 =
=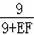
 ��
��
��EF=9=DM��
���O�İ뾶ΪR��
����Rt��EMO�У��ɹ��ɶ����ã�R2=122+��R��9��2��
��ã�R=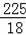
 ��
��
��EN=OM=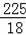
 ��9=
��9=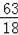
 =
=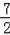
 ��
��
��AE=2EN=7��


�����������⿼���˴������������ɶ��������ε����ʺ��ж������ߵ��ж���ƽ���ߵ����ʵ�Ӧ�ã���Ҫ����ѧ���ۺ��������ʽ��������ͼ������������Ŀ�Ƚϵ��ͣ���һ���ȽϺõ���Ŀ��

 B��
B�� C��
C�� D��
D��

 ���Ա���x��ȡֵ��Χ����������������
���Ա���x��ȡֵ��Χ����������������


 B��
B��
 C��
C��
 D��
D��



 �������ǣ� ��
�������ǣ� �� ��
�� ﹣4��
﹣4�� ����1﹣
����1﹣ ��0��
��0��