题目内容
19.抛物线y=-$\frac{1}{2}$(x+3)2+1的顶点坐标是(-3,1).分析 已知抛物线的顶点式,可直接写出顶点坐标.
解答 解:∵抛物线y=-$\frac{1}{2}$(x+3)2+1,
∴顶点坐标是(-3,1).
故答案为:(-3,1).
点评 此题考查二次函数的性质,掌握顶点式y=a(x-h)2+k,顶点坐标是(h,k),对称轴是x=h,是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若关于x的方程(a-1)x2+2x-1=0是一元二次方程,则a的取值范围是( )
| A. | a≠1 | B. | a>1 | C. | a<1 | D. | a≠0 |
14.已知关于x的一元二次方程x2+x+m2-4=0的一个根是0,则m的值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 2或-2 |
11.方程x2+2x+3=0的二次项系数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
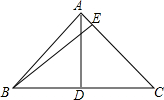 如图,在等腰△ABC中,AB=AC,底边上的高AD=10cm,腰AC上的高BE=12cm
如图,在等腰△ABC中,AB=AC,底边上的高AD=10cm,腰AC上的高BE=12cm
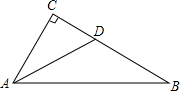 如图,∠ACB=90°,AD是∠CAB的平分线,BC=12,CD=4.5,则AC=9.
如图,∠ACB=90°,AD是∠CAB的平分线,BC=12,CD=4.5,则AC=9.