题目内容
已知x+y=4，xy=4，求代数式（x2+1）（y2+1）的值．
考点：整式的混合运算—化简求值
专题：计算题
分析：把x+y=4两边平方，利用完全平方公式化简，把xy的值代入求出x2+y2的值，原式利用多项式乘多项式法则计算，将各自的值代入计算即可求出值．
解答：解：把x+y=4两边平方得：（x+y）2=x2+y2+2xy=16，
将xy=4代入得：x2+y2=8，
则原式=（xy）2+x2+y2+1=16+8+1=25．
将xy=4代入得：x2+y2=8，
则原式=（xy）2+x2+y2+1=16+8+1=25．
点评：此题考查了整式的混合运算-化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
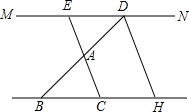已知如图，MN∥BH，BD和EC交于点A，过点D作DH∥EC交BC延长线于点H．