题目内容
3.计算:(1)7$\sqrt{2}$$+3\sqrt{8}$-5$\sqrt{50}$
(2)$\sqrt{12}$-($\sqrt{\frac{1}{3}}-\sqrt{\frac{1}{27}}$)
(3)2$\sqrt{2}$•5$\sqrt{\frac{1}{6}}$$+\frac{3}{\sqrt{3}}$
(4)(5$\sqrt{48}$-6$\sqrt{27}$+4$\sqrt{15}$)$÷\sqrt{3}$
(5)(2$\sqrt{3}$-3)2-($\sqrt{3}$-1)($\sqrt{3}$+1)
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先把各二次根式化为最简二次根式,然后去括号合并即可;
(3)先进行二次根式的乘除运算,然后合并即可;
(4)根据二次根式的除法法则运算;
(5)根据完全平方公式和平方差公式计算.
解答 解:(1)原式=7$\sqrt{2}$+6$\sqrt{2}$-25$\sqrt{2}$
=-12$\sqrt{2}$;
(2)原式=2$\sqrt{3}$-$\frac{\sqrt{3}}{3}$+$\frac{\sqrt{3}}{9}$
=$\frac{16\sqrt{3}}{9}$;
(3)原式=10$\sqrt{2×\frac{1}{6}}$+$\sqrt{3}$
=$\frac{10\sqrt{3}}{3}$+$\sqrt{3}$
=$\frac{13\sqrt{3}}{3}$;
(4)原式=5$\sqrt{48÷3}$-6$\sqrt{27÷3}$+4$\sqrt{15÷3}$
=20-18+4$\sqrt{5}$
=2+4$\sqrt{5}$;
(5)原式=12-12$\sqrt{3}$+9-(3-1)
=10-12$\sqrt{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
14.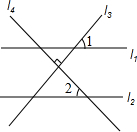 如图,直线l1∥l2,l3⊥l4,∠1=46°,那么∠2的度数为( )
如图,直线l1∥l2,l3⊥l4,∠1=46°,那么∠2的度数为( )
 如图,直线l1∥l2,l3⊥l4,∠1=46°,那么∠2的度数为( )
如图,直线l1∥l2,l3⊥l4,∠1=46°,那么∠2的度数为( )| A. | 46° | B. | 44° | C. | 23° | D. | 22° |
11.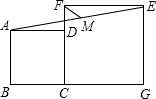 如图,正方形ABCD,正方形CGEF的边长分别为4、6,且点B、C、G在同一条直线上,点M是线段AE的中点,连接MF,则MF的长为( )
如图,正方形ABCD,正方形CGEF的边长分别为4、6,且点B、C、G在同一条直线上,点M是线段AE的中点,连接MF,则MF的长为( )
 如图,正方形ABCD,正方形CGEF的边长分别为4、6,且点B、C、G在同一条直线上,点M是线段AE的中点,连接MF,则MF的长为( )
如图,正方形ABCD,正方形CGEF的边长分别为4、6,且点B、C、G在同一条直线上,点M是线段AE的中点,连接MF,则MF的长为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{2}$ |
18.不等式(2x+1)(x-2)>3x2-x(x+2)的解集是( )
| A. | x<2 | B. | x<-2 | C. | x>-2 | D. | x>2 |
