Question

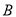（本题满分14分）如图①，在平面直角坐标系中，点的坐标为，点的坐标为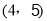，二次函数的图象记为抛物线．

（1）平移抛物线，使平移后的抛物线过两点，记为抛物线，如图②，求抛物线的函数表达式．

（2）请在图②上用尺规作图的方式探究抛物线上是否存在点，使为等腰三角形．若存在，请判断点共有几个可能的位置（保留作图痕迹）并在图中画出P点，以P1、P2、P3、、、表示不同的点；若不存在，请说明理由．

（3）设抛物线的顶点为，为抛物线一点．若，求点的坐标．

 

Answer 1

（1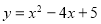） （2）5个 （3）（3,2）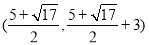

【解析】

试题分析：（1）可设出平移后的二次函数的解析式，然后将A、B的坐标代入抛物线的解析式中，即可求得l2的函数表达式．

（2）应有三点：①以A为圆心，AB为半径作弧可交抛物线l2于一点；②以B为圆心，AB为半径坐标交抛物线于另一点；③作线段AB的垂直平分线可交抛物线于两点，因此共有5个符合条件的P点．

（3）第一种情况：根据函数的对称性可以求出K点.

第二种情况：本题可通过求三角形的面积来求K的坐标．由于三角形ABC的面积无法直接求出，因此可其转换成其他规则图形面积的和差来解．分别过A、B、C三点作x轴的垂线，因此△ABC的面积可用三个直角梯形的面积差来求出．设出K的坐标，利用上面面积求法求出K的坐标.

试题解析：（1） 设抛物线l2的函数表达式为，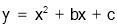

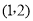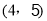把A，B代入得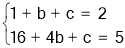

解之得b=-4，c=5

所以的解析式为.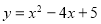

（2） 由题意可做图为

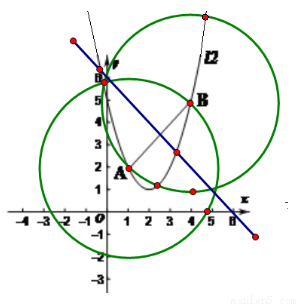
由图可以直接看出共5个点.

（3）第一种情况：因为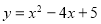，所以可求出顶点C的坐标为（2,1），根据二次函数的对称性可以知当K点和A点对称时两个三角形的面积相等，由对称轴x=2可求得K点的横坐标为3，所以K的坐标为（3,2）.

第二种情况：

由函数的解析式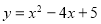可求出C的坐标（2,1），然后过ABC作垂线（如图），利用梯形的面积差可以求出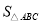=3，设K点为（x，y），同理可用面积法求出K点的坐标为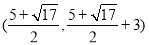和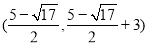，所以有三种情况，分别为（3,2）.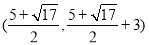

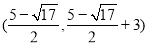考点：二次函数的图像和性质，梯形的面积，基本作图