题目内容
14.为了响应“足球进校园”的号召,某体育用品商店计划购进一批足球,第一次用6000元购进A品牌足球m个,第二次又用6000元购进B品牌足球,购进的B品牌足球的数量比购进的A品牌足球多30个,并且每个A品牌足球的进价是每个B品牌足球的进价的$\frac{5}{4}$.(1)求m的值;
(2)若这两次购进的A,B两种品牌的足球分别按照a元/个,$\frac{4}{5}$a元/个两种价格销售,全部销售完毕后,可获得的利润不低于4800元,求出a的最小值.
分析 (1)设购进A品牌足球m个,根据购进的B品牌足球的数量比购进的A品牌足球多30个,列方程求解;
(2)根据获得的利润不低于4800元,列不等式求解.
解答 解:(1)设购进A品牌足球m个,根据题意可得:$\frac{6000}{m}=\frac{5}{4}×\frac{6000}{m+30}$,
解得:m=120,
经检验m=120是原方程的解,
所以m的值是120;
(2)由(1)可得:B品牌足球的个数为150个,$\frac{6000}{120}=50$元/个,$\frac{6000}{150}$=40元/个,
A品牌足球和B品牌足球的进价分别为50元/个和40元/个,
120a+150×$\frac{4}{5}a-6000×2≥4800$,
解得:a≥70,
答:a的最小值为70.
点评 本题考查了分式方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解,注意检验.

练习册系列答案
相关题目
2.一副完整的扑克牌,去掉大小王,将剩余的52张混合后从中随机抽取一张,则抽出A的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{13}$ | D. | $\frac{1}{52}$ |
4.互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品进价为200元,按标价的五折销售,仍可获利10%,设这件商品的标价为x元,根据题意列出方程( )
| A. | 0.5x-200=10%×200 | B. | 0.5x-200=10%×0.5x | ||
| C. | 200=(1-10%)×0.5x | D. | 0.5x=(1-10%)×200 |
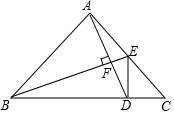 如图,在Rt△ABC中,∠BAC=90°,AB=AC,∠ABC=∠ACB,D、E分别是BC、AC上的点,若AD⊥BE,∠ADB=∠CDE,CE=2,则S△ADE=$\frac{4}{3}$.
如图,在Rt△ABC中,∠BAC=90°,AB=AC,∠ABC=∠ACB,D、E分别是BC、AC上的点,若AD⊥BE,∠ADB=∠CDE,CE=2,则S△ADE=$\frac{4}{3}$.