题目内容
11. 如图,在△ABC中,∠A=120°,AB=AC=6,点D在AB上,过点D作DE∥BC交AC于点E,现将△ADE沿着DE所在的直线折叠,使得点A落在点A′处,A′D,A′E分别交BC于点F、G.若FG:DE=1:2,则图中阴影部分的周长为( )
如图,在△ABC中,∠A=120°,AB=AC=6,点D在AB上,过点D作DE∥BC交AC于点E,现将△ADE沿着DE所在的直线折叠,使得点A落在点A′处,A′D,A′E分别交BC于点F、G.若FG:DE=1:2,则图中阴影部分的周长为( )| A. | 3$\sqrt{3}$+6 | B. | 4$\sqrt{3}$+8 | C. | 6$\sqrt{3}$+4 | D. | 8$\sqrt{3}$ |
分析 根据相似三角形的性质得到$\frac{A′F}{A′D}$=$\frac{FG}{DE}$=$\frac{1}{2}$,得到A′F=DF,推出BD=FD,得到AD=A′D=2BD,得到BD=2,同理DG=2,过A作AM⊥BC于M,求得BM=$\frac{\sqrt{3}}{2}$AB=3$\sqrt{3}$,得到BC=6$\sqrt{3}$,于是得到结论.
解答 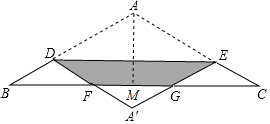 解:∵DE∥BC,
解:∵DE∥BC,
∴FG∥DE,
∴△A′FG∽△A′DE,
∴$\frac{A′F}{A′D}$=$\frac{FG}{DE}$=$\frac{1}{2}$,
∴A′F=DF,
∵∠A=120°,AB=AC,
∴∠B=∠C=30°,
∴∠ADE=∠AED=30°,
∵将△ADE沿着DE所在的直线折叠,使得点A落在点A′处,
∴∠A′DE=∠ADE=30°,
∴∠DFB=∠A′FG=30°,
∴∠B=∠DFB,
∴BD=FD,
∴AD=A′D=2BD,
∵AB=AC=6,
∴BD=2,
同理DG=2,
过A作AM⊥BC于M,
∴BM=$\frac{\sqrt{3}}{2}$AB=3$\sqrt{3}$,
∴BC=6$\sqrt{3}$,
∴DE=$\frac{2}{3}$BC=4$\sqrt{3}$,
∴FG=$\frac{1}{2}$DE=2$\sqrt{3}$,
∴图中阴影部分的周长=DE+DF+FG+EG=6$\sqrt{3}$+4,
故选C.
点评 本题考查了翻折变换(折叠问题),等腰三角形的性质,相似三角形的判定和性质,解直角三角形,熟练掌握折叠的性质是解题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
19.确定一个圆的条件是( )
| A. | 已知圆心 | B. | 已知半径 | ||
| C. | 过三个已知点 | D. | 过一个三角形的三个顶点 |
20.某科技公司研发出一款多型号的智能手表,一家代理商出售该公司的A型智能手表,去年销售总额为80000元,今年A型智能手表的售价每只比去年降了600元,若售出的数量与去年相同,销售总额将比去年减少25%.
(1)请问今年A型智能手表每只售价多少元?
(2)今年这家代理商准备新进一批A型智能手表和B型智能手表共100只,它们的进货价与销售价格如右表,若B型智能手表进货量不超过A型智能手表数量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
| A型智能手表 | B型智能手表 | |
| 进价 | 1300元/只 | 1500元/只 |
| 售价 | 今年的售价 | 2300元/只 |
(2)今年这家代理商准备新进一批A型智能手表和B型智能手表共100只,它们的进货价与销售价格如右表,若B型智能手表进货量不超过A型智能手表数量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
1. 如图所示,直线l1∥l2,三角尺的一个顶点在l2上,若∠1=70°,则∠2=( )
如图所示,直线l1∥l2,三角尺的一个顶点在l2上,若∠1=70°,则∠2=( )
 如图所示,直线l1∥l2,三角尺的一个顶点在l2上,若∠1=70°,则∠2=( )
如图所示,直线l1∥l2,三角尺的一个顶点在l2上,若∠1=70°,则∠2=( )| A. | 70° | B. | 60° | C. | 40° | D. | 30° |
 人的记忆会随着时间的推移而淡化,遗忘曲线(记住的内容和时间的关系)如图所示,请根据图象回答下列问题:
人的记忆会随着时间的推移而淡化,遗忘曲线(记住的内容和时间的关系)如图所示,请根据图象回答下列问题: