题目内容
3.如果0°<θ<90°,且|sin2θ-$\frac{1}{4}$|+(cosθ-$\frac{\sqrt{3}}{2}$)2=0,求tanθ的值.分析 根据非负数的和为零,可得每个非负数同时为零,根据特殊角三角函数值,可得θ的值,根据特殊角的正切值,可得答案.
解答 解:由0°<θ<90°,且|sin2θ-$\frac{1}{4}$|+(cosθ-$\frac{\sqrt{3}}{2}$)2=0,得
|sin2θ-$\frac{1}{4}$=0,cosθ-$\frac{\sqrt{3}}{2}$0,
解得θ=30°,
tanθ=tan30°=$\frac{\sqrt{3}}{3}$.
点评 本题考查了特殊角三角函数值,利用非负数的和为零得出每个非负数同时为零是解题关键,熟记特殊角三角函数值是解题关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
15.两条直线相交时,若有一个角为锐角,则另外三个角都是( )
| A. | 3个都是锐角 | B. | 2锐角,1个钝角 | C. | 3个钝角 | D. | 1个锐角,2个钝角 |
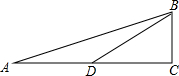 已知,如图,在Rt△ABC中,∠BCA=90°,∠A=15°,D是AC边上一点,BC=$\frac{1}{2}$BD.求证:点D在AB的垂直平分线上.
已知,如图,在Rt△ABC中,∠BCA=90°,∠A=15°,D是AC边上一点,BC=$\frac{1}{2}$BD.求证:点D在AB的垂直平分线上.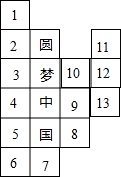 从下图中的正方形中选两个涂色,使这两个正方形与4个写有汉字的正方形一起,折叠后能围成一个正方体,则你所涂的正方形是2和9(只填数字即可).
从下图中的正方形中选两个涂色,使这两个正方形与4个写有汉字的正方形一起,折叠后能围成一个正方体,则你所涂的正方形是2和9(只填数字即可).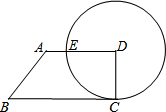 如图,已知四边形ABCD中,AD∥BC,∠C=90°,∠B=45°,以D为圆心,DC为半径的圆交AD于点E.若AB=2$\sqrt{2}$,AD=2$\sqrt{3}$,判断直线AB与⊙D位置关系,并说明理由.
如图,已知四边形ABCD中,AD∥BC,∠C=90°,∠B=45°,以D为圆心,DC为半径的圆交AD于点E.若AB=2$\sqrt{2}$,AD=2$\sqrt{3}$,判断直线AB与⊙D位置关系,并说明理由.