题目内容
如图，点A，B，C在⊙O上，已知∠ABC=130°，则∠AOC=（ ）| A、100° | B、110° |
| C、120° | D、130° |
考点：圆周角定理
专题：
分析：在优弧AC上取点D，连接AD，CD，根据圆内接四边形的性质求出∠D的度数，由圆周角定理即可得出结论．
解答：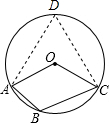
解：在优弧AC上取点D，连接AD，CD，
∵四边形ABCD是圆内接四边形，∠ABC=130°，
∴∠D=180°-10°=50°．
∵∠D与∠AOC是同弧所对的圆周角与圆心角，
∴∠AOC=2∠D=100°．
故选A．
解：在优弧AC上取点D，连接AD，CD，∵四边形ABCD是圆内接四边形，∠ABC=130°，
∴∠D=180°-10°=50°．
∵∠D与∠AOC是同弧所对的圆周角与圆心角，
∴∠AOC=2∠D=100°．
故选A．
点评：本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
如图，正六边形ABCDEF内接于⊙O，若⊙O的内接正△ACE的面积为48已知：当x=1时，代数式
ax3-3bx+4的值是7，那么，当x=-1时，这个代数式的值是（ ）
| 1 |
| 2 |
| A、7 | B、3 | C、1 | D、-7 |
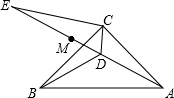如图，在△ABC中，AC=BC，∠ACB=90°，点D为△ABC内一点，∠CAD=∠CBD=15°，E为AD延长线上的一点，且CE=CA．已知⊙O的半径为2，圆心O到直线l的距离PO=1，则直线l与⊙O的位置关系是（ ）
| A、相切 | B、相离 |
| C、相交 | D、无法判断 |