题目内容
 如图,AB∥x轴,分别交双曲线y=
如图,AB∥x轴,分别交双曲线y=| 1 |
| x |
| 2 |
| x |
考点:反比例函数系数k的几何意义
专题:
分析:先根据反比例函数系数k的几何意义得出S△AOD与S△BOD的面积,进而可得出结论.
解答: 解:∵AB∥x轴,分别交双曲线y=
解:∵AB∥x轴,分别交双曲线y=
和y=-
于A、B,
∴AB⊥y轴,
∴S△AOD=
×|-2|=1,S△BOD=
×1=
,
∴S△ABO=S△AOD+S△BOD
=1+
=
.
 解:∵AB∥x轴,分别交双曲线y=
解:∵AB∥x轴,分别交双曲线y=| 1 |
| x |
| 2 |
| x |
∴AB⊥y轴,
∴S△AOD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABO=S△AOD+S△BOD
=1+
| 1 |
| 2 |
=
| 3 |
| 2 |
点评:本题考查的是反比例函数系数k的几何意义,熟知在反比例函数y=
的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是
,且保持不变是解答此题的关键.
| k |
| x |
| |k| |
| 2 |

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )| A、a<0 |
| B、c>0 |
| C、b2-4ac>0 |
| D、当x<2时,函数值y随x增大而增大;当x>2时,函数值y随x增大而减小 |
已知扇形的圆心角为120°,半径为6cm,则扇形的面积为( )
| A、12cm2 |
| B、36cm2 |
| C、12πcm2 |
| D、36πcm2 |
已知⊙O的半径为2,圆心O到直线l的距离PO=1,则直线l与⊙O的位置关系是( )
| A、相切 | B、相离 |
| C、相交 | D、无法判断 |
下列命题中,正确的是( )
| A、全等三角形的高相等 |
| B、全等三角形的中线相等 |
| C、全等三角形的角平分线相等 |
| D、全等三角形对应边上的高相等 |
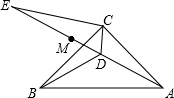 如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.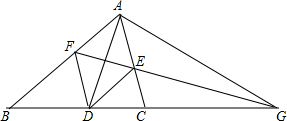 如图,AD是∠BAC的平分线,DE平行AB交AC于点E,DF平行AC交AB于点F,延长FE交BC的延长线于点G,求证:
如图,AD是∠BAC的平分线,DE平行AB交AC于点E,DF平行AC交AB于点F,延长FE交BC的延长线于点G,求证: