题目内容
 如图,抛物线y=ax2-2ax+2(a>0)与y轴交于点C,过C作CD∥x轴交抛物线于点D,则点D的坐标为
如图,抛物线y=ax2-2ax+2(a>0)与y轴交于点C,过C作CD∥x轴交抛物线于点D,则点D的坐标为考点:二次函数图象上点的坐标特征
专题:
分析:先确定点C坐标,再求出对称轴,根据点C与点D两点关于对称轴对称,即可得出点D坐标.
解答:解:∵抛物线y=ax2-2ax+2(a>0)与y轴交于点C,
∴C(0,2),
∵CD∥x轴,
∴点C与点D两点关于对称轴对称,
∴点D坐标(2,2),
故答案为(2,2).
∴C(0,2),
∵CD∥x轴,
∴点C与点D两点关于对称轴对称,
∴点D坐标(2,2),
故答案为(2,2).
点评:本题考查了二次函数图象上的点的坐标特征,熟记二次函数的顶点坐标(-
,
).
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
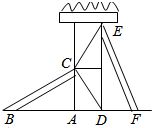 如图,有两个长度相等的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向上的长度DF相等,若∠ABC=32°,则∠DFE的度数为( )
如图,有两个长度相等的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向上的长度DF相等,若∠ABC=32°,则∠DFE的度数为( )| A、32° | B、28° |
| C、58° | D、45° |
 如图,在Rt△ABC中,∠C=90°,∠ABC=40°,将△ABC绕点A顺时针旋转α得到△ADE(0°<α<90°)连接CE交AB于点F.
如图,在Rt△ABC中,∠C=90°,∠ABC=40°,将△ABC绕点A顺时针旋转α得到△ADE(0°<α<90°)连接CE交AB于点F. 如图所示为六月份某水库的水位图.由于从5号连续降雨,7号到达警戒水位20m,于是从7号开始开闸泻洪,并加固加高堤坝,10号到达30m的危险水位时停止了下雨,水位开始回落.请回答下列问题:
如图所示为六月份某水库的水位图.由于从5号连续降雨,7号到达警戒水位20m,于是从7号开始开闸泻洪,并加固加高堤坝,10号到达30m的危险水位时停止了下雨,水位开始回落.请回答下列问题: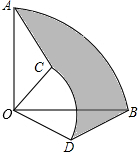 如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=6,OC=2,分别连结AC、BD,则图中阴影部分的面积为
如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=6,OC=2,分别连结AC、BD,则图中阴影部分的面积为