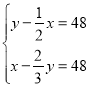题目内容
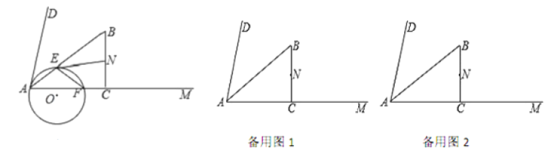
【题目】探究:如图①,点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 外,连结
外,连结![]() .过线段
.过线段![]() 的中点
的中点![]() 作
作![]() ,交
,交![]() 的平分线
的平分线![]() 于点
于点![]() ,连结
,连结![]() .求证:
.求证:![]() .
.
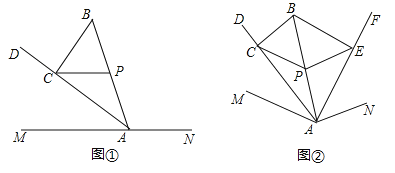
应用:如图②,点![]() 在
在![]() 内部,连结
内部,连结![]() .过线段
.过线段![]() 的中点
的中点![]() 作
作![]() ,交
,交![]() 的平分线
的平分线![]() 于点
于点![]() ;作
;作![]() ,交
,交![]() 的平分线
的平分线![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() .若
.若![]() ,则
,则![]() 的大小为多少度.
的大小为多少度.
【答案】探究:详见解析;应用:![]() 的大小为105度.
的大小为105度.
【解析】
探究:先根据角平分线的定义、平行线的性质得出![]() ,再根据等腰三角形的定义、线段的中点定义得出
,再根据等腰三角形的定义、线段的中点定义得出![]() ,然后根据等腰三角形的性质得出
,然后根据等腰三角形的性质得出![]() ,最后根据三角形的内角和定理、角的和差可得
,最后根据三角形的内角和定理、角的和差可得![]() ,即可得证;
,即可得证;
应用:先根据探究的结论可得![]() ,再根据角平分线的定义、直角三角形的性质即可得.
,再根据角平分线的定义、直角三角形的性质即可得.
探究:![]() 是
是![]() 的平分线
的平分线
![]()
![]()
![]()
![]()
![]()
![]() 点
点![]() 是线段AB的中点
是线段AB的中点
![]()
![]()
![]()
![]()
![]() ,即
,即![]()
![]()
![]()
![]() ;
;
应用:![]() 平分
平分![]() ,
,![]() 平分
平分![]()
![]()
![]()
![]()
由探究的结论得:![]()
![]() 和
和![]() 是直角三角形
是直角三角形
![]()
两式相加得:![]()
![]() ,即
,即![]()
解得![]()
即![]() 的大小为105度.
的大小为105度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目