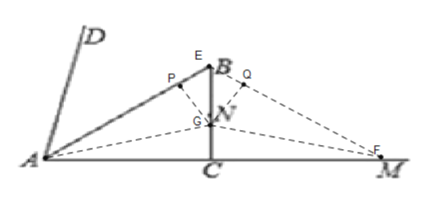
题目内容
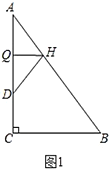
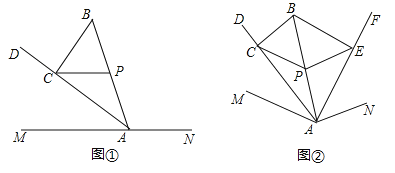
【题目】如图，在
内部做
，
平分，
，
，
，点
为
的中点：动点
由
出发，沿运动，速度为每秒5个单位，动点
由出发，沿
运动，速度为每秒8个单位，当点到达点
时，两点同时停止运动；过、、作
；
（1）判断
的形状为________，并判断
与的位置关系为__________；
（2）求
为何值时，
与相切？求出此时的半径，并比较半径与劣弧
长度的大小；
（3）直接写出的内心运动的路径长为__________；（注：当、、重合时，内心就是点）
（4）直接写出线段与有两个公共点时，的取值范围为__________．
（参考数据：
，
，
，
，
）
【答案】（1）△AEF为等腰三角形；DA与
相切；（2）劣弧
长度＞半径；（3）
的内心运动的路径长为
；（4）线段
与有两个公共点时，
的取值范围为
.
【解析】
（1）过点E作EH⊥AF于点H，连接OH，OA，证明△AEH∽△ABC，得到AH=FH，即可证明为等腰三角形；根据圆周角和圆心角证明∠DAC=∠AOE，即可证明∠DAO=90°；
（2）连接EO，AO，OF，交AC于点H，根据相切知四边形EHCN为矩形，从而求出t，在Rt△AOH中，根据勾股定理求出半径，然后求出∠AOH的度数即可比较；
（3）得到的内心运动的路径长为AG，然后根据面积求出内切圆半径，从而求出AG长；
（4）分别讨论两种极限位置，①当MN与相切时，②当N在圆上时，即ON为半径，分别求出t的值，即可确定t的取值范围.
解：（1）过点E作EH⊥AF于点H，连接OH，OA，
∵
，
，
，
∴
，
设运动时间为t，
∴AE=5t，AF=8t，
∵EH⊥AF，
∴△AEH∽△ABC，
∴
，即
，
∴
，
∴FH=4t，
∴AH=FH，
∴△AEF为等腰三角形；
∴E为
的中点，
∴H为AF的中点，
∴OH垂直AC，
∴∠OAF+∠AOE=90°，
∴∠AOE=2∠EFA，
∵AB平分∠DAC，∠EAC=∠EFA，
∴∠DAC=∠AOE，
∴∠DAC+∠AOE=90°，
∴∠DAO=90°，
∴DA与相切；
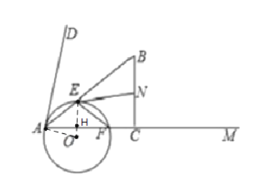
（2）连接EO，AO，OF，交AC于点H，
由（1）知EH⊥AC，
∵EN与相切，
∴∠OEN=90°，
∴四边形EHCN为矩形，
在Rt△AHE中，
，
∴NC=EH=3t，
∵N是BC中点，
∴BC=6t，
∵BC=6，
∴6t=6，
解得：t=1，
∴AH=4，EH=3，
设半径为x，
∴OH=x-3，
在Rt△AOH中，
，
∴
，
解得：
，
∴
，
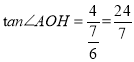∴∠AOH=74°，
∴∠AOH＞60°，
∴AE＞半径，
∴劣弧长度＞半径；
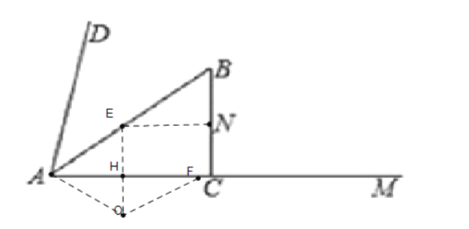
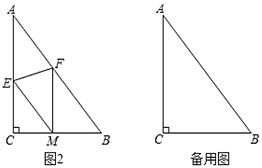
（3）当E运动到B点时，
t=10÷5=2，
∴AF=2×8=16，
此时△AEF的内心记为G，
当A、E、F三点重合时，内心为A，
∴的内心运动的路径长为AG，
作GP⊥AE于点P，GQ⊥EF于点Q，
S△AEF=
，
设CG=a，
∴S△AEF=S△AGF+S△AEG+S△FEG，
∴
，
解得：
，
在Rt△ACG中，
，即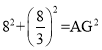
，
∴AG=，
∴的内心运动的路径长为；
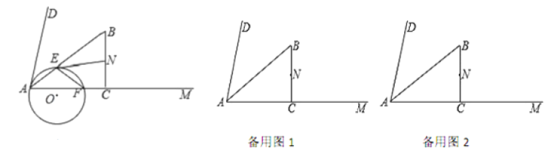
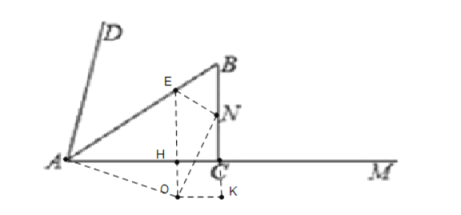
（4）分别讨论两种极限位置，
①当MN与相切时，
由（2）知，t=1；
②当N在圆上时，即ON为半径，如图所示：
则OE=ON，
∴AH=4t，EH=3t，
设半径为x，
则在Rt△AOH中，
，
解得：
，
∴CK=OH=
,
在Rt△OKN中，
，
∴
，
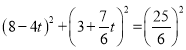解得：
，
∴线段与有两个公共点时，的取值范围为.
