题目内容
19．
如图，每个小正方形的边长都为1．（1）求四边形ABCD的面积与周长；
（2）∠DAB是直角吗？
分析 （1）利用四边形ABCD所在矩形面积-周围三角形面积进而求出其面积，再利用勾股定理得出其周长即可；
（2）连接BD，利用勾股定理的逆定理求出∠DAB是直角即可．
解答 解：
（1）四边形ABCD的面积为：25-1-$\frac{1}{2}$×1×5-$\frac{1}{2}$×1×4-$\frac{1}{2}$×1×2-$\frac{1}{2}$×2×4=14.5；
周长为：AB+BC+CD+AD=$\sqrt{26}$+$\sqrt{5}$+$\sqrt{17}$+$\sqrt{20}$=3$\sqrt{5}$+$\sqrt{17}$+$\sqrt{26}$；
（2）∠DAB是直角，理由如下：
连接BD，
∵AB2+AD2=20+5=25，BD2=25，
∴AB2+AD2=BD2，
∴△ABD是直角三角形，
∴∠BAD是直角．
点评 此题主要考查了勾股定理以及勾股定理的逆定理，正确应用勾股定理是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
10．
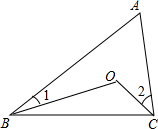如图，点O是△ABC内一点，∠A=80°∠1=15°，∠2=40°，则∠BOC的度数为（ ）
如图，点O是△ABC内一点，∠A=80°∠1=15°，∠2=40°，则∠BOC的度数为（ ）| A． | 45° | B． | 55° | C． | 135° | D． | 150° |
4．
如图，点A0位于坐标原点，点A1，A2，A3，…，A2015在y轴的正半轴上，点B1，B2，B3，…，B2015在二次函数$y=\frac{2}{3}{x^2}$位于第一象限的图象上，△A0B1A1，△A1B2A2，△A2B3A3，…，△A2014B2015A2015都是等边三角形，则△A2014B2015A2015的边长为（ ）
如图，点A0位于坐标原点，点A1，A2，A3，…，A2015在y轴的正半轴上，点B1，B2，B3，…，B2015在二次函数$y=\frac{2}{3}{x^2}$位于第一象限的图象上，△A0B1A1，△A1B2A2，△A2B3A3，…，△A2014B2015A2015都是等边三角形，则△A2014B2015A2015的边长为（ ）| A． | 2014 | B． | 2015 | C． | $2014\sqrt{3}$ | D． | $2015\sqrt{3}$ |