题目内容
14.在四张背面完全相同的卡片正面分别画有正三角形、正六边形、平行四边形和圆,将这四张卡片背面朝上放在桌面上,现从中随机抽取一张后放回,再从中随机抽取一张,两次抽出的图形都是中心对称图形的概率是$\frac{9}{16}$.分析 用A表示正三角形,B表示正六边形,C表示平行四边形,D表示圆,画出树状图展示所有16种等可能的结果数,再找出两次抽出的图形都是中心对称图形的结果数,然后根据概率公式求解.
解答 解:画树状图:A表示正三角形,B表示正六边形,C表示平行四边形,D表示圆,
共有16种等可能的结果数,其中两次抽出的图形都是中心对称图形占9种,
所以两次抽出的图形都是中心对称图形的概率=$\frac{9}{16}$.
故答案为$\frac{9}{16}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求事件A或B的概率.也考查了中心对称图形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.据报道,滕州市某小区居民李先生改进用水设备,在十年内帮助他居住小区的居民累计节水30万吨,将30万用科学记数法表示应为( )
| A. | 0.3×106 | B. | 3×105 | C. | 3×106 | D. | 30×104 |
6.据报道,参观某会展的人数达35.6万,用科学记数法表示数35.6万是( )
| A. | 3.56×101 | B. | 3.56×104 | C. | 3.56×105 | D. | 35.6×104 |
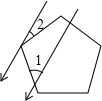 如图,一束平行太阳光照射到正五边形上,若∠1=46°,则∠2=26°.
如图,一束平行太阳光照射到正五边形上,若∠1=46°,则∠2=26°.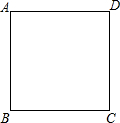 如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)
如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)