题目内容
11.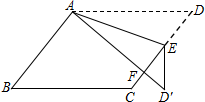 如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=52°,∠DAE=20°,则∠FED′的大小为( )
如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=52°,∠DAE=20°,则∠FED′的大小为( )| A. | 20° | B. | 30° | C. | 36° | D. | 40° |
分析 由平行四边形的性质得出∠D=∠B=52°,由折叠的性质得:∠D′=∠D=52°,∠EAD′=∠DAE=20°,由三角形的外角性质求出∠AEF=72°,与三角形内角和定理求出∠AED′=108°,即可得出∠FED′的大小.
解答 解:∵四边形ABCD是平行四边形,
∴∠D=∠B=52°,
由折叠的性质得:∠D′=∠D=52°,∠EAD′=∠DAE=20°,
∴∠AEF=∠D+∠DAE=52°+20°=72°,∠AED′=180°-∠EAD′-∠D′=108°,
∴∠FED′=108°-72°=36°;
故答案为:36°.
点评 本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理;熟练掌握平行四边形的性质和折叠的性质,求出∠AEF和∠AED′是解决问题的关键.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
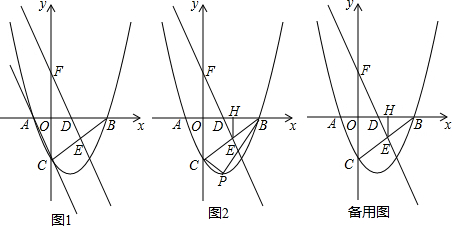
6. 如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)b<0;(4)a+b+c<0.你认为其中错误的有( )
如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)b<0;(4)a+b+c<0.你认为其中错误的有( )
 如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)b<0;(4)a+b+c<0.你认为其中错误的有( )
如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)b<0;(4)a+b+c<0.你认为其中错误的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 1个 |
3.若x=0是关于x的一元二次方程(a+2)x2-$\sqrt{a-2}$x+a2+a-6=0的一个根,则a的值是( )
| A. | a≠-2 | B. | a=2 | C. | a=-3 | D. | a=-3或a=2 |