题目内容
20.如果△ABC的三个顶点A,B,C所对的边分别为a,b,c,那么下列条件中,不能判断△ABC是直角三角形的是( )| A. | ∠A=15°,∠B=75° | B. | ∠A:∠B:∠C=1:2:3 | C. | a=$\sqrt{2}$,b=$\sqrt{3}$,c=$\sqrt{5}$ | D. | a=6,b=10,c=12 |
分析 利用直角三角形的定义和勾股定理的逆定理逐项判断即可.
解答 解:
A、由条件可得∠A+∠B=15°+75°=90°,∴∠C=90°,故△ABC为直角三角形;
B、B、设∠A=x°,∠B=2x°,∠C=3x°,
x+2x+3x=180,
解得:x=30,
则3x°=90°,
是直角三角形,故此选项不合题意;
C、由条件可得到a2+b2=c2,满足勾股定理的逆定理,故△ABC是直角三角形;
D、由条件有a2+b2=c2,不满足勾股定理的逆定理,故△ABC不是直角三角形;
故选D.
点评 本题主要考查直角三角形的判定方法,掌握判定直角三角形的方法是解题的关键,可以利用定义也可以利用勾股定理的逆定理.

练习册系列答案
相关题目
11. 如图,梯子的各条横档互相平行,若∠1=80°,则∠2的度数是( )
如图,梯子的各条横档互相平行,若∠1=80°,则∠2的度数是( )
 如图,梯子的各条横档互相平行,若∠1=80°,则∠2的度数是( )
如图,梯子的各条横档互相平行,若∠1=80°,则∠2的度数是( )| A. | 80° | B. | 100° | C. | 110° | D. | 120° |
15. 实数a,b在数轴上的位置如图所示,以下说法正确的是( )
实数a,b在数轴上的位置如图所示,以下说法正确的是( )
 实数a,b在数轴上的位置如图所示,以下说法正确的是( )
实数a,b在数轴上的位置如图所示,以下说法正确的是( )| A. | b<a | B. | ab>0 | C. | |b|<|a| | D. | a+b=0 |
5.若分式$\frac{x}{x-3}$有意义,则x应满足的条件是( )
| A. | x≠3 | B. | x<3 | C. | x≠3且x≠0 | D. | x≠0 |
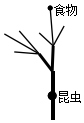 一只昆虫在如图所示的树枝上寻觅食物,假定昆虫在每个岔路口都会随机地选择一条路径,则它获得食物的概率是$\frac{1}{6}$.
一只昆虫在如图所示的树枝上寻觅食物,假定昆虫在每个岔路口都会随机地选择一条路径,则它获得食物的概率是$\frac{1}{6}$.