题目内容
9.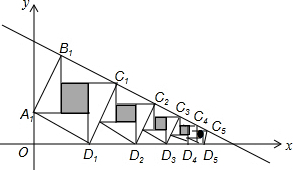 赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x轴和y轴,大正方形的顶点B1、C1、C2、C3、…、Cn在直线y=-$\frac{1}{2}$x+$\frac{7}{2}$上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为$({\frac{2}{3})}^{2n-2}$.
赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x轴和y轴,大正方形的顶点B1、C1、C2、C3、…、Cn在直线y=-$\frac{1}{2}$x+$\frac{7}{2}$上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为$({\frac{2}{3})}^{2n-2}$.
分析 设第n个大正方形的边长为an,则第n个阴影小正方形的边长为$\frac{\sqrt{5}}{5}$an,根据一次函数图象上点的坐标特征即可求出直线y=-$\frac{1}{2}$x+$\frac{7}{2}$与y轴的交点坐标,进而即可求出a1的值,再根据相似三角形的性质即可得出an=$(\frac{2}{3})^{n-1}$a1=$\sqrt{5}$$(\frac{2}{3})^{n-1}$,结合正方形的面积公式即可得出结论.
解答 解:设第n个大正方形的边长为an,则第n个阴影小正方形的边长为$\frac{\sqrt{5}}{5}$an,
当x=0时,y=-$\frac{1}{2}$x+$\frac{7}{2}$=$\frac{7}{2}$,
∴$\frac{7}{2}$=$\frac{\sqrt{5}}{5}$a1+$\frac{\sqrt{5}}{2}$a1,
∴a1=$\sqrt{5}$.
∵a1=a2+$\frac{1}{2}$a2,
∴a2=$\frac{2}{3}$$\sqrt{5}$,
同理可得:a3=$\frac{2}{3}$a2,a4=$\frac{2}{3}$a3,a5=$\frac{2}{3}$a4,…,
∴an=$(\frac{2}{3})^{n-1}$a1=$\sqrt{5}$$(\frac{2}{3})^{n-1}$,
∴第n个阴影小正方形的面积为$(\frac{\sqrt{5}}{5}{a}_{n})^{2}$=$[(\frac{2}{3})^{n-1}]^{2}$=$(\frac{2}{3})^{2n-2}$.
故答案为:$(\frac{2}{3})^{2n-2}$.
点评 本题考查了相似三角形的判定与性质、一次函数图象上点的坐标特征以及正方形的面积,找出第n个大正方形的边长为an=$(\frac{2}{3})^{n-1}$a1=$\sqrt{5}$$(\frac{2}{3})^{n-1}$是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 5 | B. | -5 | C. | 1 | D. | -1 |
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 等边三角形 |
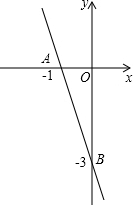 已知:点A(-1,0),B(0,-3).
已知:点A(-1,0),B(0,-3).
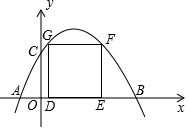 如图,抛物线l与坐标轴的交点为A(-1,0),B(4,0),C(0,2),四边形DEFG是正方形,且点D,E在x轴上,点F,G在抛物线上,则正方形DEFG的面积为57±8$\sqrt{41}$.
如图,抛物线l与坐标轴的交点为A(-1,0),B(4,0),C(0,2),四边形DEFG是正方形,且点D,E在x轴上,点F,G在抛物线上,则正方形DEFG的面积为57±8$\sqrt{41}$.