题目内容
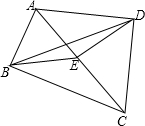 如图,四边形ABCD是由一个锐角为30°的直角△ABC与一个等腰直角△ACD拼成,E为斜边AC的中点.
如图,四边形ABCD是由一个锐角为30°的直角△ABC与一个等腰直角△ACD拼成,E为斜边AC的中点.(1)判断线段BE、DE的大小,并说明理由
(2)求∠BDE的大小.
考点:直角三角形斜边上的中线
专题:
分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得BE=DE=
AC;
(2)求出∠BED的度数,再根据等腰三角形两底角相等列式计算即可得解.
| 1 |
| 2 |
(2)求出∠BED的度数,再根据等腰三角形两底角相等列式计算即可得解.
解答:解:(1)∵E为斜边AC的中点,
∴BE=DE=
AC,
∴BE=DE;
(2)由题意得,∠BAC=90°-30°=60°,
所以,∠AEB=∠BAC=60°,
∠AED=90°,
所以,∠BED=60°+90°=150°,
所以,∠BDE=
×(180°-150°)=15°.
∴BE=DE=
| 1 |
| 2 |
∴BE=DE;
(2)由题意得,∠BAC=90°-30°=60°,
所以,∠AEB=∠BAC=60°,
∠AED=90°,
所以,∠BED=60°+90°=150°,
所以,∠BDE=
| 1 |
| 2 |
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰直角三角形的性质,等腰三角形的性质,熟记各性质是解题的关键.

练习册系列答案
相关题目
某种商品现在每件售价为200元,计划经过两年把价格降为112.5元,则平均每年降低的百分率为( )
| A、25% | B、20% |
| C、30% | D、15% |
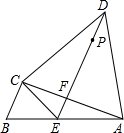 某小区有A、B、C、D四栋居民楼,经测量发现A、C、D三栋居民楼两两距离相等,且∠ACB=90°,物业打算在A、B两楼之间的小路AB上修建一个休闲运动区域E,且D楼居民恰好能沿着小路DE直达该区域,小路DE和小路AC恰好互相垂直,垂足为F.
某小区有A、B、C、D四栋居民楼,经测量发现A、C、D三栋居民楼两两距离相等,且∠ACB=90°,物业打算在A、B两楼之间的小路AB上修建一个休闲运动区域E,且D楼居民恰好能沿着小路DE直达该区域,小路DE和小路AC恰好互相垂直,垂足为F.