题目内容
4.(1)如果$\frac{a}{b}$=$\frac{c}{d}$=…=$\frac{m}{n}$=k(b+d+…+n≠0),那么$\frac{a+c+…+m}{b+d+…+n}$=k成立吗?为什么?(2)在△ABC和△A′B′C′中,$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$=$\frac{CA}{C′A′}$=$\frac{1}{2}$,且△ABC的周长为15cm,求△A′B′C′的周长.
分析 (1)只有当b+d+…+n≠0时才成立;
(2)求出$\frac{AB+BC+CA}{A′B′+B′C′+C′A′}$=$\frac{AB}{A′B′}$=$\frac{1}{2}$,把△ABC的周长为15cm代入,即可求出答案.
解答 解:(1)不成立,
理由是:只有当b+d+…+n≠0时,才成立;
(2)∵在△ABC和△A′B′C′中,$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$=$\frac{CA}{C′A′}$=$\frac{1}{2}$,
∴$\frac{AB+BC+CA}{A′B′+B′C′+C′A′}$=$\frac{AB}{A′B′}$=$\frac{1}{2}$,
∵△ABC的周长为15cm,
∴AB+BC+CA=30cm,
∴△A′B′C′的周长是30cm.
点评 本题考查了比例性质的应用,能灵活运用性质进行推理是解此题的关键,注意:如果$\frac{a}{b}$=$\frac{c}{d}$,那么ad=bc.

练习册系列答案
相关题目
2. 如图,数轴上有A,B,C,D四个点,其中互为相反数的数对应的点是( )
如图,数轴上有A,B,C,D四个点,其中互为相反数的数对应的点是( )
 如图,数轴上有A,B,C,D四个点,其中互为相反数的数对应的点是( )
如图,数轴上有A,B,C,D四个点,其中互为相反数的数对应的点是( )| A. | 点A与点C | B. | 点A与点D | C. | 点B与点C | D. | 点B与点D |
14.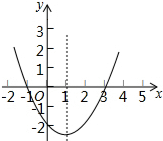 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
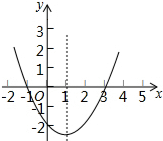 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )| A. | 函数有最小值 | B. | 当-1<x<3时,y>0 | ||
| C. | 当x<1时,y随x的增大而减小 | D. | 对称轴是直线x=1 |
 动手画一画,请把下图补成以A为对称中心的中心对称图形.
动手画一画,请把下图补成以A为对称中心的中心对称图形.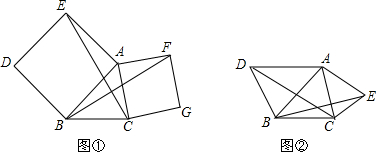
 如图,已知CD⊥DA,DA⊥AB,∠1=∠2,问直线DE与AF是否平行?为什么?
如图,已知CD⊥DA,DA⊥AB,∠1=∠2,问直线DE与AF是否平行?为什么? ,实际车牌号为100968.
,实际车牌号为100968.