题目内容
8．一个多边形的每个内角都相等，且一个外角比一个内角大60°，求这个多边形的每个内角的度数及边数．分析 一个多边形的每个内角都相等，且一个外角比一个内角大60°，又由于内角与外角的和是180度．设内角是x°，外角是y°，列方程组求解即可．
解答 解：设内角是x°，外角是y°，
则得到一个方程组$\left\{\begin{array}{l}{y-x=60}\\{x+y=180}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x=60}\\{y=120}\end{array}\right.$．
而任何多边形的外角是360°，
则多边形中外角的个数是360÷120=3，
故这个多边形的每个内角的度数是60°，边数是三边形．
点评 本题考查了根据多边形的内角与外角的关系转化为方程组的问题，并利用了多边形的外角和定理；已知外角求边数的这种方法是需要熟记的内容．
练习册系列答案
相关题目
1．某产品每件成本10元，试销阶段每件产品的销售价x（元）与产品的日销售量y（件）之间的关系如表：
已知日销售量y是销售价x的一次函数．
（1）求日销售量y（件）与每件产品的销售价x（元）之间的函数表达式；
（2）当每件产品的销售价定为35元时，此时每日的销售利润是多少元？
| x/元 | … | 15 | 20 | 25 | … |
| y/件 | … | 25 | 20 | 15 | … |
（1）求日销售量y（件）与每件产品的销售价x（元）之间的函数表达式；
（2）当每件产品的销售价定为35元时，此时每日的销售利润是多少元？
16．下面关于平方根的说法中正确的是（ ）
| A． | 任何数都有两个平方根 | B． | 若a＞0，x2=a，则x是a的一个平方根 | ||
| C． | 2的平方根是4 | D． | 若a＞0，x2=a，则a是x的一个平方根 |
3．
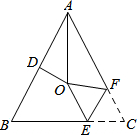如图，△ABC中，AB=AC，∠BAC=54°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC的度数是（ ）
如图，△ABC中，AB=AC，∠BAC=54°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC的度数是（ ）| A． | 106° | B． | 108° | C． | 110° | D． | 112° |
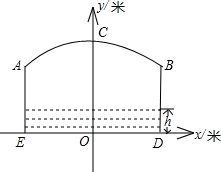如图，小河上有一拱桥，拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE、ED、DB组成，已知河底ED是水平的，ED=16米，AE=8米，抛物线的顶点C到ED的距离是11米，以ED所在的直线为x轴，抛物线的对称轴为y轴建立平面直角坐标系．
18．下列图案中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |