题目内容
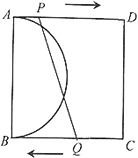
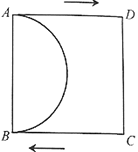
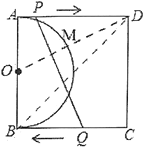
【题目】如图，在正方形ABCD中，
，以AB为直径作半圆O，点P从点A出发，沿AD方向以每秒1个单位的速度向点D运动，点Q从点C出发，沿C8方向以每秒3个单位的速度向点B运动，两点同时开始运动，当一点到达终点后，另一点也随之停止运动。设运动时间为
.
(1)设点M为半圆
上任意一点，则DM的最大值为______，最小值为______.
(2)设PQ交半圆于点F和点G(点F在点G的上方)，当
时，求
的长度；
(3)在运动过程中，PQ和半圆能否相切？若相切，请求出此时l的值，若不能相切，请说明理由；
(4)点N是半圆上一点，且
，当运动时，PQ与半圆的交点恰好为点N，直接写出此时t的值。
【答案】(1)
，
；(2)4
；(3)不能相切；(4)当运动
时，
与半圆
的交点恰好为点
.
【解析】
(1) 找出DM最大和最小的位置，即可得出结论；（2）先确定出AP=3，进而得出∠OFE=30°，即可得出∠FOG=120°，最后用弧长公式即可得出结论；（3）假设PQ与半圆相切，进而表示出PQ=12-2t．QH=12-4t，再用勾股定理建立122+（12-4t）2=（12-2t）2，判断出出此方程无解，即可得出结论．(4)先判断出0≤t≤4，再利用S扇形BON=6π，求出∠BON=60°，再判断出AP始终小于AI，最后得出
，建立方程即可得出结论．
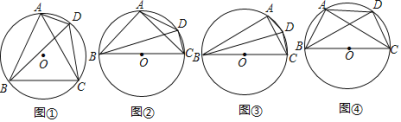
解：(1)如图，连接OD，此时DM最小，
在
中，
，
；
当点M和点B重合时，连接BD，
DM最大
，
故答案为：
，
(2)
四边形ABCD是正方形，
，
，
当
时，四边形ABQP是矩形，
，
∵
，
，
，
，解得
，
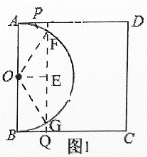
如图1，设PQ交半圆于F，G，过点O作
于点E，连接OF、OG，
，
∵
，
，
∵
，
，
∴
的长度
(3)不能相切．
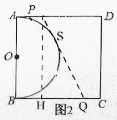
理由：若PQ与半圆O相切，设切点为点S，如图2，
由切线长定理，得
，
，
．
过点P作
于点H，
四边形APHB是矩形，
，
，
∵在
中，
，
即：
.
∵
，此方程无解，
在运动过程中，
和半圆不能相切；
(4)∵点
是以每秒3个单位的速度向点
运动，
.
，
∵点
是以每秒1个单位的速度向点
运动，
即
.
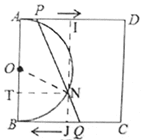
如图3，过点作
，交
于点
，交
于点
，过点作
于点
，则四边形
和四边形
都是矩形，
∵
，
.
∵
，
，
.
当点
运动到点时，
，不符合题意，
始终小于
，
，
，
∵
，，
，
.
∵
，
.
，解得
，
∵
，
当运动
时，与半圆的交点恰好为点.
