题目内容
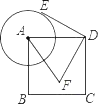
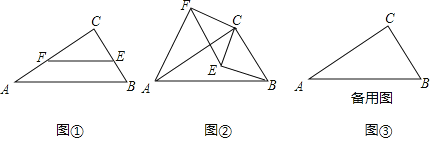
【题目】如图,点![]() 分别在正三角形
分别在正三角形![]() 的三边上,且
的三边上,且![]() 也是正三角形.若
也是正三角形.若![]() 的边长为
的边长为![]() ,
,![]() 的边长为
的边长为![]() ,则
,则![]() 的内切圆半径为__________.
的内切圆半径为__________.
【答案】![]()
【解析】
根据△ABC、△EFD都是等边三角形,可证得△AEF≌△BDE≌△CDF,即可求得AE+AF=AE+BE=a,然后根据切线长定理得到AH=![]() (AE+AF-EF)=
(AE+AF-EF)=![]() (a-b);,再根据直角三角形的性质即可求出△AEF的内切圆半径.
(a-b);,再根据直角三角形的性质即可求出△AEF的内切圆半径.
解:如图1,⊙I是△ABC的内切圆,由切线长定理可得:AD=AE,BD=BF,CE=CF,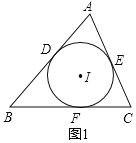
∴AD=AE=![]() [(AB+AC)-(BD+CE)]=
[(AB+AC)-(BD+CE)]=![]() [(AB+AC)-(BF+CF)]=
[(AB+AC)-(BF+CF)]=![]() (AB+AC-BC),
(AB+AC-BC),
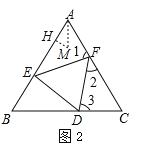
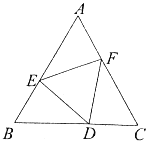
如图2,∵△ABC,△DEF都为正三角形,
∴AB=BC=CA,EF=FD=DE,∠BAC=∠B=∠C=∠FED=∠EFD=∠EDF=60°,
∴∠1+∠2=∠2+∠3=120°,∠1=∠3;
在△AEF和△CFD中,
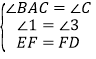 ,
,
∴△AEF≌△CFD(AAS);
同理可证:△AEF≌△CFD≌△BDE;
∴BE=AF,即AE+AF=AE+BE=a.
设M是△AEF的内心,过点M作MH⊥AE于H,
则根据图1的结论得:AH=![]() (AE+AF-EF)=
(AE+AF-EF)=![]() (a-b);
(a-b);
∵MA平分∠BAC,
∴∠HAM=30°;
∴HM=AHtan30°=![]() (a-b)
(a-b)![]() =
=![]()
故答案为:![]() .
.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目